Bài 7.42 trang 65 Toán 11 tập 2 Kết nối tri thức

Bài 7.42 trang 65 Toán 11 Tập 2 Kết nối tri thức:

Cho hình hộp ABCD.A'B'C'D' có độ dài tất cả các cạnh bằng a, AA' ⊥ (ABCD) và $\widehat{BAD}$ = 60^o.

a) Tính thể tích của khối hộp ABCD.A'B'C'D'.

b) Tính khoảng cách từ A đến mặt phẳng (A'BD).

Kiến Thức Cần Nhớ

• Thể tích hình hộp: ⁸$V = S_{đáy} \cdot h$. Vì ⁹$AA' \perp (ABCD)$nên ¹⁰$AA'$chính¹¹ là chiều cao $h$ 

• Diện tích hình thoi: $S = AB \cdot AD \cdot \sin(\widehat{BAD})$.

• Khoảng cách từ điểm đến mặt phẳng: Sử dụng phương pháp dựng mặt phẳng phụ vuông góc với mặt phẳng mục tiêu (mô hình 3 đường vuông góc).

Giải bài 7.42 trang 65 Toán 11 Tập 2 Kết nối tri thức:

Ta có hình minh hoạ như sau:

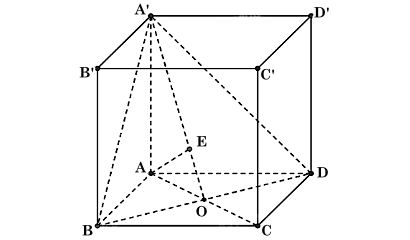
a) Gọi O là giao điểm của AC và BD.

Vì hình hộp ABCD.A'B'C'D' có độ dài tất cả các cạnh bằng a nên ABCD là hình thoi,

⇒ AO = OC và AC  ⊥ BD.

Có S_ABD = $\frac{1}{2}$.AO.BD = $\frac{1}{2}.CO.BD = S_BCD.

Nên S_ABCD = 2S_ABD.

Mà S_ABD = $\frac{1}{2}.AB.AD.sin$\widehat{BAD}$ = $\frac{1}{2}.a.a.sin60^o $= \frac{a^2\sqrt{3}}{4}$ .

⇒ S_ABCD = $\frac{a^2\sqrt{3}}{2}$

Vậy, ta có:

$V_{ABCD.A'B'C'D'}=AA'.S_{ABCD}$ $=a.\frac{a^2\sqrt{3}}{2}$ $=\frac{a^3\sqrt{3}}{2}$

b) Vì AO ⊥ BD mà AA' ⊥ (ABCD) nên AA' ⊥ BD.

Do đó BD ⊥ (AOA').

⇒ (A'BD) ⊥ (AOA').

Kẻ AE ⊥ A'O tại E. Vì (A'BD) ⊥ (AOA'), (A'BD) ∩ (AOA') = A'O và AE ⊥ A'O nên AE ⊥ (A'BD).

Do đó d(A, (A'BD)) = AE.

Xét tam giác ABD có AB = AD = a nên tam giác ABD là tam giác cân tại A

mà $\widehat{BAD}=60^o$ nên tam giác ABD đều,

⇒ BD = a

mà $BO=\frac{1}{2}BD=\frac{a}{2}$

Xét tam giác AOB vuông tại O, có:

$AO=\sqrt{AB^2-BO^2}$ $=\sqrt{a^2-\frac{a^2}{4}}$ $=\frac{a\sqrt{3}}{2}$

Vì AA' ⊥ (ABCD) nên AA' ⊥ AO hay tam giác A'AO vuông tại A.

Xét Δ A'AO vuông tại A có:

$\frac{1}{AE^2}=\frac{1}{AA'^2}+\frac{1}{AO^2}$ $=\frac{1}{a^2}+\frac{4}{3a^2}$ $=\frac{7}{3a^2}$ $\Rightarrow AE=a\sqrt{\frac{3}{7}}$

Vậy $d( A,(A'BD))=a\sqrt{\frac{3}{7}}$