Bài 7.38 trang 65 Toán 11 tập 2 Kết nối tri thức

Bài 7.38 trang 65 Toán 11 Tập 2 Kết nối tri thức:

Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = a, OB = $a\sqrt{2}$ và OC = 2a. Tính khoảng cách từ điểm O đến mặt phẳng ABC.

Kiến Thức Cần Nhớ

• Tính chất tứ diện vuông: Nếu $OA, OB, OC$ đôi một vuông góc tại $O$, thì $O$ được gọi là chân đường cao hạ từ $O$ xuống mặt phẳng đối diện $(ABC)$.

• Hệ thức lượng trong tam giác vuông: Trong tam giác vuông, nghịch đảo bình phương đường cao bằng tổng nghịch đảo bình phương hai cạnh góc vuông:

  $\frac{1}{h^2} = \frac{1}{a^2} + \frac{1}{b^2}$

• Công thức nhanh cho tứ diện vuông: Khoảng cách $h$ từ $O$ đến mặt phẳng $(ABC)$ thỏa mãn:

  $\frac{1}{h^2} = \frac{1}{OA^2} + \frac{1}{OB^2} + \frac{1}{OC^2}$

Giải bài 7.38 trang 65 Toán 11 Tập 2 Kết nối tri thức:

Ta có hình minh hoạ như sau:

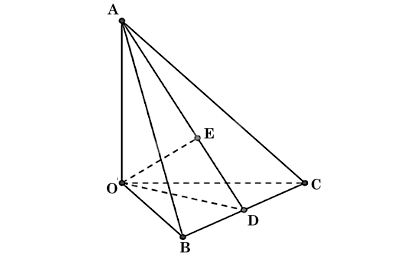
Kẻ OD ⊥ BC tại D.

Có OA ⊥ OB, OA ⊥ OC nên OA ⊥ (OBC),

⇒ OA ⊥ BC mà OD ⊥ BC nên BC ⊥ (OAD).

Kẻ OE ⊥ AD tại E.

Vì BC ⊥ (OAD) nên BC ⊥ OE mà OE ⊥ AD nên OE ⊥ (ABC).

⇒ d(O, (ABC)) = OE.

Xét ΔOBC vuông tại O, OD là đường cao có:

$\frac{1}{OD^2}=\frac{1}{OB^2}+\frac{1}{OC^2}$ $=\frac{1}{2a^2}+\frac{1}{4a^2}=\frac{3}{4a^2}$

Vì OA ⊥ (OBC) nên OA ⊥ OD.

Xét tam giác AOD vuông tại O, OE là đường cao nên

$\frac{1}{OE^2}=\frac{1}{OA^2}+\frac{1}{OD^2}$ $=\frac{1}{a^2}+\frac{3}{4a^2}=\frac{7}{4a^2}$ $\Rightarrow OE=\frac{2a\sqrt{7}}{7}$

Vậy $d(O, (ABC))=\frac{2a\sqrt{7}}{7}$