Bài 7.41 trang 65 Toán 11 tập 2 Kết nối tri thức

Bài 7.41 trang 65 Toán 11 Tập 2 Kết nối tri thức:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a. Biết tam giác SAD vuông cân tại S và (SAD) ⊥ (ABCD).

a) Tính theo a thể tích của khối chóp S.ABCD.

b) Tính khoảng cách giữa hai đường thẳng AD và SC.

Kiến Thức Cần Nhớ

• Đường cao hình chóp: Nếu hai mặt phẳng vuông góc với nhau, đường thẳng nào nằm trong mặt này và vuông góc với giao tuyến thì vuông góc với mặt kia.

• Thể tích khối chóp: $V = \frac{1}{3} \cdot S_{đáy} \cdot h$.

• Khoảng cách giữa hai đường thẳng chéo nhau: Nếu $d_1 // (P)$ và $d_2 \subset (P)$ thì $d(d_1, d_2) = d(d_1, (P))$.

Giải bài 7.41 trang 65 Toán 11 Tập 2 Kết nối tri thức:

Ta có hình minh hoạ như sau:

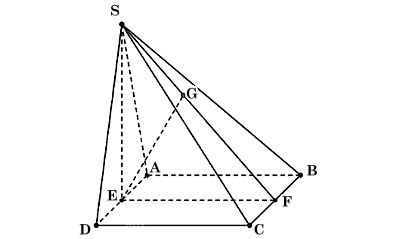
a) Kẻ SE ⊥ AD tại E. Vì tam giác SAD vuông cân tại S nên E là trung điểm của AD.

Có (SAD) ⊥ (ABCD), (SAD) ∩ (ABCD) = AD,

SE ⊥ AD nên SE ⊥ (ABCD).

Vì tam giác SAD vuông cân tại S, SE là trung tuyến nên:

$SE=\frac{1}{2}AD=\frac{a}{2}$

Khi đó: 

$V_{S.ABCD}=\frac{1}{3}S_{ABCD}.SE$ $=\frac{1}{3}.a^2.\frac{a}{2}$ $=\frac{a^3}{6}$

b) Vì ABCD là hình vuông nên AD // BC mà BC ⊂ (SBC) nên AD // (SBC).

Khi đó d(AD, SC) = d(AD, (SBC)) = d(E, (SBC)).

Kẻ EF // AB (F thuộc BC).

Khi đó EF ⊥ BC (vì A ⊥ BC).

Mà SE ⊥ (ABCD) nên SE ⊥ BC mà EF ⊥ BC nên BC ⊥ (SEF).

Lại có BC ⊂ (SBC) nên (SBC) ⊥ (SEF) và (SBC) ∩ (SEF) = SF.

Kẻ EG ⊥ SF tại G nên EG ⊥ (SBC).

Khi đó d(E, (SBC)) = EG.

Vì ABCD là hình vuông nên EF = AB = a.

Xét ΔSEF vuông tại E, EG là đường cao, có:

$\frac{1}{EG^2}=\frac{1}{SE^2}+\frac{1}{EF^2}$ $=\frac{4}{a^2}+\frac{1}{a^2}=\frac{5}{a^2}$ $\Rightarrow EG=\frac{a\sqrt{5}}{5}$

Vậy $d(AD,SC)=\frac{a\sqrt{5}}{5}$