Bài 7.5 trang 36 Toán 11 tập 2 Kết nối tri thức

Bài 7.5 trang 36 Toán 11 tập 2 Kết nối tri thức:

Cho hình chóp S.ABC có đáy là tam giác cân tại A và SA ⊥ (ABC). Gọi M là trung điểm của BC. Chứng minh rằng:

a) BC ⊥ (SAM)

b) Tam giác SBC cân tại S.

Phân tích và Phương pháp giải

Để giải quyết bài toán này, chúng ta cần vận dụng các định lý và tính chất hình học sau:

• Chứng minh đường thẳng vuông góc với mặt phẳng: Một đường thẳng được gọi là vuông góc với mặt phẳng nếu nó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng đó.

• Tính chất tam giác cân: Trong tam giác cân, đường trung tuyến ứng với cạnh đáy đồng thời là đường cao.

• Định lý liên quan: Nếu một đường thẳng vuông góc với mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.

• Nhận biết tam giác cân: Một tam giác có đường trung tuyến đồng thời là đường cao thì tam giác đó là tam giác cân.

Giải bài 7.5 trang 36 Toán 11 tập 2 Kết nối tri thức:

* Cần nhớ: Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng một mặt phẳng thì nó vuông góc với mặt phẳng đó.

Ta có hình minh họa như sau:

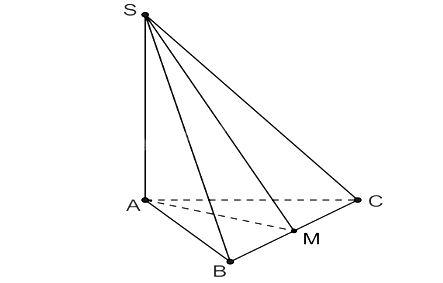
a) Chứng minh BC ⊥ (SAM)

Xét ΔABC cân tại A có

AM là đường trung tuyến (M là trung điểm BC)

⇒ AM là đường cao 

⇒ AM ⊥ BC   (1)

Lại có: SA ⊥ BC (vì SA ⊥ (ABC)) (2)

AM ∩ SA = {A}  (3)

Từ (1), (2) và (3) ⇒ BC ⊥ (SAM) (đpcm)

b) Chứng minh: Tam giác SBC cân tại S.

Theo câu a) ta có: BC ⊥ (SAM)

Mà SM ⊂ (SAM)

⇒ BC ⊥ SM

Xét ΔSBC có:

• SM là đường cao (vì BC ⊥ SM)

• SM là đường trung tuyến (M là trung điểm BC)

⇒ Tam giác SBC cân tại S (đpcm)