Bài 7.3 trang 30 Toán 11 tập 2 Kết nối tri thức

Bài 7.3 trang 30 Toán 11 tập 2 Kết nối tri thức:

Cho tứ diện ABCD có $\widehat{CBD}=90^0$.

a) Gọi M, N tương ứng là trung điểm của AB, AD. Chứng minh rằng MN vuông góc BC.

b) Gọi G, K tương ứng là trọng tâm của các tam giác ABC, ACD. Chứng minh rằng GK vuông góc với BC.

Kiến Thức Cần Nhớ

• Đường trung bình: Đường thẳng nối trung điểm hai cạnh của tam giác thì song song với cạnh thứ ba.

• Định lý Ta-lét đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh đó các đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại.

• Quan hệ giữa tính song song và vuông góc: Nếu đường thẳng $a$ vuông góc với đường thẳng $b$, và $a$ song song với $a'$, thì $a'$ cũng vuông góc với $b$.

Giải bài 7.3 trang 30 Toán 11 tập 2 Kết nối tri thức:

* Cần nhớ: Nếu đường thẳng a vuông góc với đường thẳng b thì a vuông góc với các đường thẳng song song với b.

Ta có hình minh hoạ như sau:

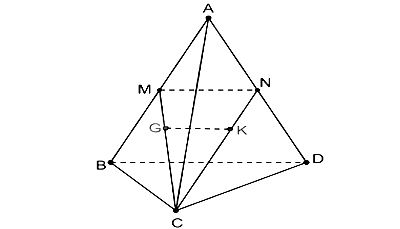
a) Chứng minh rằng MN vuông góc BC.

Xét ΔABD có

M, N tương ứng là trung điểm của AB, AD

⇒ MN là đường trung bình của tam giác ABD 

⇒ MN // BD mà BD ⊥ BC (vì $\widehat{CBD}=90^0$)

⇒ MN ⊥ BC (đpcm)

b) Chứng minh rằng GK vuông góc với BC.

Vì G, K tương ứng là trọng tâm của các tam giác ABC, ACD nên

$\frac{CG}{CM}=\frac{CK}{CN}=\frac{2}{3}$

⇒ GK // MN (Định lý Talet) mà MN ⊥ BC

⇒ GK ⊥ BC (đpcm)