Bài 6.34 trang 25 Toán 11 tập 2 Kết nối tri thức

Bài 6.34 trang 25 Toán 11 tập 2 Kết nối tri thức:

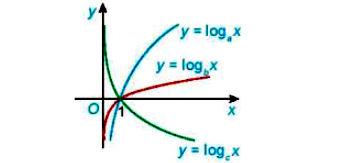
Cho đồ thị ba hàm số y = log_ax, y = log_bx và y = log_cx như hình bên. Mệnh đề nào sau đây là đúng?

A. a > b > c.

B. b > a > c.

C. a > c > b.

D. b > c > a.

Phân tích Tính chất Đồ thị Logarit

1. Tính Đơn điệu:

   • Nếu hàm số đồng biến (đồ thị đi lên), cơ số $\mathbf{a > 1}$.

   • Nếu hàm số nghịch biến (đồ thị đi xuống), cơ số $\mathbf{0 < a < 1}$.

2. So sánh Cơ số ($a > 1$): Đối với các hàm đồng biến, trên khoảng $x > 1$, đồ thị nào nằm phía dưới (gần trục $Ox$ hơn) thì có cơ số lớn hơn. (Tức là tốc độ tăng trưởng chậm hơn $\Rightarrow$ cơ số lớn hơn). Hoặc cách khác: Với $x > 1$, hàm nào có giá trị $\log_a x$ nhỏ hơn thì $a$ lớn hơn.

Giải bài 6.34 trang 25 Toán 11 tập 2 Kết nối tri thức:

* Đáp án: B.

Quan sát đồ thị ta thấy:

• Hàm số y = log_ax và y = log_bx đồng biến trên (0; + ∞) nên a, b > 1.

• Hàm số y = log_cx nghịch biến trên (0; + ∞) nên c < 1.

• Với x > 1, ta có log_ax > log_bx 

$\Leftrightarrow \frac{1}{log_ax}<\frac{1}{log_bx}$

⇔ log_xa < log_xb

⇔ a < b.

Vậy c < a < b hay b > a > c.