Bài 7.12 trang 42 Toán 11 tập 2 Kết nối tri thức
Bài tập 7.12, trang 42 SGK Toán 11 Tập 2 (Kết nối tri thức), là bài toán nâng cao về Hình học không gian, yêu cầu xác định hình chiếu vuông góc của một điểm và tính góc giữa đường thẳng và mặt phẳng trong hình chóp $S.ABC$ có cạnh bên $SA$ vuông góc với mặt đáy.
Bài 7.12 trang 42 Toán 11 Tập 2 Kết nối tri thức
Cho hình chóp S.ABC có SA ⊥ (ABC), tam giác ABC vuông tại B, SA = AB = BC = a.
a) Xác định hình chiếu của A trên mặt phẳng (SBC).
b) Tính góc giữa SC và mặt phẳng (ABC).
Phân tích Phương pháp Giải
-
Phần a (Hình chiếu của $A$): Để tìm hình chiếu $I$ của $A$ lên $(SBC)$, ta cần chứng minh $AI \perp (SBC)$. Ta thường sử dụng định lý ba đường vuông góc.
-
Chứng minh $BC \perp (SAB)$.
-
Kẻ $AI \perp SB$.
-
Chứng minh $AI \perp (SBC)$.
-
-
Phần b (Tính góc): Góc giữa $SC$ và $(ABC)$ là góc giữa $SC$ và hình chiếu của nó trên $(ABC)$, tức là $\mathbf{\widehat{SCA}}$. Ta dùng tỉ số lượng giác trong tam giác vuông $SAC$.
Giải bài 7.12 trang 42 Toán 11 Tập 2 Kết nối tri thức
Ta có hình minh hoạ như sau:
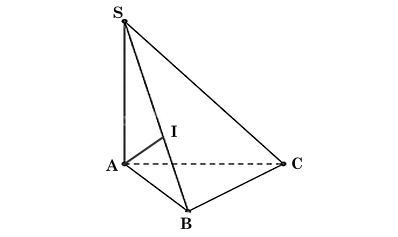
a) Kẻ AI ⊥ SB tại I.
Vì SA ⊥ (ABC) nên SA ⊥ BC.
Mặt khác, ABC là tam giác vuông tại B nên AB ⊥ BC mà SA ⊥ BC,
⇒ BC ⊥ (SAB).
Vì BC ⊥ (SAB) nên BC ⊥ AI mà AI ⊥ SB nên AI ⊥ (SBC).
Vậy I là hình chiếu của A trên mặt phẳng (SBC).
b) Vì SA ⊥ (ABC) nên AC là hình chiếu của SC trên mặt phẳng (ABC).
Khi đó góc giữa SC và mặt phẳng (ABC) bằng góc giữa hai đường thẳng AC và SC
Mà $(AC, SC) = \widehat{SCA}$
Xét tam giác ABC vuông tại B có:
$AC=\sqrt{AB^2+BC^2}$ $=\sqrt{a^2+a^2}=a\sqrt{2}$
Vì SA ⊥ (ABC) nên SA ⊥ AC.
Xét tam giác SAC vuông tại A, có:
$tan\widehat{SCA}=\frac{SA}{AC}$ $=\frac{a}{a\sqrt{2}}=\frac{1}{\sqrt{2}}$
$\Rightarrow \widehat{SCA}=35,26^o$
Vậy góc giữa SC và mặt phẳng (ABC) khoảng 35,26°.
Như vậy, ta có kết quả sau:
| Yêu cầu | Phương pháp | Kết quả |
| a) Hình chiếu của $A$ trên $(SBC)$ | Chứng minh $BC \perp (SAB)$, sau đó kẻ $AI \perp SB$ | $\mathbf{I}$ (với $AI \perp SB$) |
| b) Góc giữa $SC$ và $(ABC)$ | $\text{Góc} = \widehat{SCA}$. Tính $\tan(\widehat{SCA}) = \frac{SA}{AC}$ | $\mathbf{\approx 35,26^\circ}$ |
• Xem thêm:
Đánh giá & nhận xét
-
 Bài 7.9 trang 36 Toán 11 tập 2 Kết nối tri thức
Bài 7.9 trang 36 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.8 trang 36 Toán 11 tập 2 Kết nối tri thức
Bài 7.8 trang 36 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.7 trang 36 Toán 11 tập 2 Kết nối tri thức
Bài 7.7 trang 36 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.6 trang 36 Toán 11 tập 2 Kết nối tri thức
Bài 7.6 trang 36 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.5 trang 36 Toán 11 tập 2 Kết nối tri thức
Bài 7.5 trang 36 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.45 trang 65 Toán 11 tập 2 Kết nối tri thức
Bài 7.45 trang 65 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.44 trang 65 Toán 11 tập 2 Kết nối tri thức
Bài 7.44 trang 65 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.43 trang 65 Toán 11 tập 2 Kết nối tri thức
Bài 7.43 trang 65 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.42 trang 65 Toán 11 tập 2 Kết nối tri thức
Bài 7.42 trang 65 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.41 trang 65 Toán 11 tập 2 Kết nối tri thức
Bài 7.41 trang 65 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.40 trang 65 Toán 11 tập 2 Kết nối tri thức
Bài 7.40 trang 65 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.39 trang 65 Toán 11 tập 2 Kết nối tri thức
Bài 7.39 trang 65 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.38 trang 65 Toán 11 tập 2 Kết nối tri thức
Bài 7.38 trang 65 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.4 trang 30 Toán 11 tập 2 Kết nối tri thức
Bài 7.4 trang 30 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.3 trang 30 Toán 11 tập 2 Kết nối tri thức
Bài 7.3 trang 30 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.2 trang 30 Toán 11 tập 2 Kết nối tri thức
Bài 7.2 trang 30 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.1 trang 30 Toán 11 tập 2 Kết nối tri thức
Bài 7.1 trang 30 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.15 trang 43 Toán 11 tập 2 Kết nối tri thức
Bài 7.15 trang 43 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.14 trang 43 Toán 11 tập 2 Kết nối tri thức
Bài 7.14 trang 43 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.13 trang 43 Toán 11 tập 2 Kết nối tri thức
Bài 7.13 trang 43 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.11 trang 42 Toán 11 tập 2 Kết nối tri thức
Bài 7.11 trang 42 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.10 trang 42 Toán 11 tập 2 Kết nối tri thức
Bài 7.10 trang 42 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.40 trang 26 Toán 11 tập 2 Kết nối tri thức
Bài 6.40 trang 26 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.39 trang 26 Toán 11 tập 2 Kết nối tri thức
Bài 6.39 trang 26 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.38 trang 26 Toán 11 tập 2 Kết nối tri thức
Bài 6.38 trang 26 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.37 trang 26 Toán 11 tập 2 Kết nối tri thức
Bài 6.37 trang 26 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.36 trang 26 Toán 11 tập 2 Kết nối tri thức
Bài 6.36 trang 26 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.35 trang 26 Toán 11 tập 2 Kết nối tri thức
Bài 6.35 trang 26 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.34 trang 25 Toán 11 tập 2 Kết nối tri thức
Bài 6.34 trang 25 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.33 trang 25 Toán 11 tập 2 Kết nối tri thức
Bài 6.33 trang 25 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.32 trang 25 Toán 11 tập 2 Kết nối tri thức
Bài 6.32 trang 25 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.31 trang 25 Toán 11 tập 2 Kết nối tri thức
Bài 6.31 trang 25 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.30 trang 25 Toán 11 tập 2 Kết nối tri thức
Bài 6.30 trang 25 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.29 trang 25 Toán 11 tập 2 Kết nối tri thức
Bài 6.29 trang 25 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.28 trang 25 Toán 11 tập 2 Kết nối tri thức
Bài 6.28 trang 25 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.27 trang 25 Toán 11 tập 2 Kết nối tri thức: Quy tắc tính toán với lũy thừa
Bài 6.27 trang 25 Toán 11 tập 2 Kết nối tri thức: Quy tắc tính toán với lũy thừa
-
 Bài 6.26 trang 24 Toán 11 tập 2 Kết nối tri thức
Bài 6.26 trang 24 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.25 trang 24 Toán 11 tập 2 Kết nối tri thức
Bài 6.25 trang 24 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.24 trang 24 Toán 11 tập 2 Kết nối tri thức: Vận dụng hàm số mũ và logarit giải toán
Bài 6.24 trang 24 Toán 11 tập 2 Kết nối tri thức: Vận dụng hàm số mũ và logarit giải toán


















































