Bài 7.43 trang 65 Toán 11 tập 2 Kết nối tri thức

Bài 7.43 trang 65 Toán 11 Tập 2 Kết nối tri thức:

Cho hình lăng trụ ABCD.A'B'C'D'. Biết A'.ABCD là hình chóp đều có tất cả các cạnh đều bằng nhau và bằng a. Tính theo a thể tích của khối lăng trụ ABCD.A'B'C'D' và thể tích của khối chóp A'.BB'C'C.

Kiến Thức Cần Nhớ

• Hình chóp đều: Đường cao của hình chóp đều đi qua tâm của đáy.

• Thể tích khối lăng trụ: $V_{lăng trụ} = S_{đáy} \cdot h$ (với $h$ là khoảng cách giữa hai đáy).

• Thể tích khối chóp: $V_{chóp} = \frac{1}{3} \cdot S_{đáy} \cdot h$.

• Mối liên hệ: Nếu một khối chóp và một khối lăng trụ có cùng đáy và cùng chiều cao thì thể tích khối chóp bằng $1/3$ thể tích khối lăng trụ.

Giải bài 7.43 trang 65 Toán 11 Tập 2 Kết nối tri thức:

Ta có hình minh hoạ như sau:

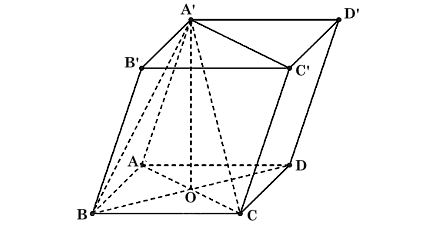
Gọi O là giao điểm của AC và BD.

Vì A'.ABCD là hình chóp đều có tất cả các cạnh đều bằng nhau và bằng a nên A'O ⊥ (ABCD).

Vì ABCD là hình vuông cạnh a nên S_ABCD = a².

Xét tam giác ABC vuông tại B, có:

$AC=\sqrt{AB^2+BC^2}$ $=\sqrt{a^2+a^2}=a\sqrt{2}$

mà O là trung điểm của AC nên:

$AO=\frac{1}{2}AC=\frac{a\sqrt{2}}{2}$

Xét tam giác A'AO vuông tại O, có:

$A'O=\sqrt{A'A^2+AO^2}$ $=\sqrt{a^2-\frac{a^2}{2}}=\frac{a\sqrt{2}}{2}$

Khi đó, ta có:

V_{ABCD.A'B'C'D'} = A'O.S_ABCD $=\frac{a\sqrt{2}}{2}.a^2=\frac{a^3\sqrt{2}}{2}$

Ta có: V_{ABCD.A'B'C'D'} = V_{AA'D'D.BB'C'C} $=\frac{a^3\sqrt{2}}{2}$

Khi đó ta thấy khối chóp A'.BB'C'C và khối lăng trụ AA'D'D.BB'C'C có chung đường cao và đáy nên:

$V_{A'.BB'C'C}=\frac{1}{3}.V_{AA'D'D.BB'C'C}$ $=\frac{1}{3}.\frac{a^3\sqrt{2}}{2}=\frac{a^3\sqrt{2}}{6}$