Bài 7.6 trang 36 Toán 11 tập 2 Kết nối tri thức
Trong hình học không gian, việc xác định tính chất của các mặt bên trong hình chóp là một kỹ năng quan trọng. Bài 7.6 trang 36 SGK Toán 11 Tập 2 kết nối tri thức yêu cầu chúng ta chứng minh tất cả các mặt bên của một hình chóp có cạnh bên vuông góc với đáy chữ nhật đều là tam giác vuông. Đây là bài toán nền tảng giúp học sinh hiểu rõ hơn về mối quan hệ giữa đường thẳng vuông góc với mặt phẳng và ứng dụng của nó trong việc xác định các góc vuông không gian.
Bài 7.6 trang 36 Toán 11 tập 2 Kết nối tri thức:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và SA ⊥ (ABCD). Chứng minh rằng các mặt bên của hình chóp S.ABCD là các tam giác vuông.
Phân tích và Phương pháp giải
Để chứng minh một tam giác là tam giác vuông, ta cần chỉ ra tam giác đó có một góc bằng $90^\circ$ (hai cạnh vuông góc với nhau). Các kiến thức trọng tâm cần vận dụng bao gồm:
-
Định nghĩa: Nếu $d \perp (P)$ thì $d$ vuông góc với mọi đường thẳng nằm trong $(P)$.
-
Điều kiện chứng minh đường thẳng vuông góc mặt phẳng: Nếu đường thẳng $d$ vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng $(P)$ thì $d \perp (P)$.
-
Tính chất hình chữ nhật: Các góc ở đỉnh của hình chữ nhật đều là góc vuông ($AB \perp BC, AD \perp CD$).
Giải bài 7.6 trang 36 Toán 11 tập 2 Kết nối tri thức:
* Cần nhớ: - Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng một mặt phẳng thì nó vuông góc với mặt phẳng đó. Định nghĩa đường thẳng vuông góc mặt phẳng.
Ta có hình minh họa như sau: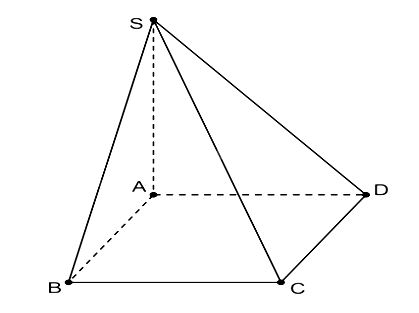
Ta có: BC ⊥ AB (vì ABCD là HCN)
BC ⊥ SA (vì SA ⊥ (ABCD))
AB ∩ SA = {A}
⇒ BC ⊥ (SAB) mà SB ⊂ (SAB)
⇒ BC ⊥ SB
Tương tự, ta có:
CD ⊥ AD (vì ABCD là HCN)
CD ⊥ SA (vì SA ⊥ (ABCD))
AD ∩ SA = {A}
⇒ CD ⊥ (SAD) mà SD ⊂ (SAD)
⇒ CD ⊥ SD
• Xét ΔSAB có: SA ⊥ AB (vì SA ⊥ (ABCD))
⇒ ΔSAB vuông tại A
• Xét ΔSBC có: SB ⊥ BC
⇒ ΔSBC vuông tại B
• Xét ΔSCD có: SD ⊥ CD
⇒ ΔSCD vuông tại C
• Xét ΔSAD có: SA ⊥ AD (vì SA ⊥ (ABCD))
⇒ ΔSAD vuông tại A
Vậy các mặt bên của hình chóp S.ABCD là các tam giác vuông.
Sau khi chứng minh, ta có kết quả về các đỉnh vuông của các mặt bên như sau:
| Mặt bên | Đỉnh vuông | Lý do chính |
| $\triangle SAB$ | $A$ | $SA \perp AB$ |
| $\triangle SAD$ | $A$ | $SA \perp AD$ |
| $\triangle SBC$ | $B$ | $BC \perp SB$ |
| $\triangle SCD$ | $D$ | $CD \perp SD$ |
Kết luận chung: Tất cả các mặt bên của hình chóp $S.ABCD$ đều là các tam giác vuông. (đpcm)
• Xem thêm:
Đánh giá & nhận xét
-
 Bài 7.9 trang 36 Toán 11 tập 2 Kết nối tri thức
Bài 7.9 trang 36 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.8 trang 36 Toán 11 tập 2 Kết nối tri thức
Bài 7.8 trang 36 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.7 trang 36 Toán 11 tập 2 Kết nối tri thức
Bài 7.7 trang 36 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.5 trang 36 Toán 11 tập 2 Kết nối tri thức
Bài 7.5 trang 36 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.45 trang 65 Toán 11 tập 2 Kết nối tri thức
Bài 7.45 trang 65 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.44 trang 65 Toán 11 tập 2 Kết nối tri thức
Bài 7.44 trang 65 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.43 trang 65 Toán 11 tập 2 Kết nối tri thức
Bài 7.43 trang 65 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.42 trang 65 Toán 11 tập 2 Kết nối tri thức
Bài 7.42 trang 65 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.41 trang 65 Toán 11 tập 2 Kết nối tri thức
Bài 7.41 trang 65 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.40 trang 65 Toán 11 tập 2 Kết nối tri thức
Bài 7.40 trang 65 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.39 trang 65 Toán 11 tập 2 Kết nối tri thức
Bài 7.39 trang 65 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.38 trang 65 Toán 11 tập 2 Kết nối tri thức
Bài 7.38 trang 65 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.4 trang 30 Toán 11 tập 2 Kết nối tri thức
Bài 7.4 trang 30 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.3 trang 30 Toán 11 tập 2 Kết nối tri thức
Bài 7.3 trang 30 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.2 trang 30 Toán 11 tập 2 Kết nối tri thức
Bài 7.2 trang 30 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.1 trang 30 Toán 11 tập 2 Kết nối tri thức
Bài 7.1 trang 30 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.15 trang 43 Toán 11 tập 2 Kết nối tri thức
Bài 7.15 trang 43 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.14 trang 43 Toán 11 tập 2 Kết nối tri thức
Bài 7.14 trang 43 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.13 trang 43 Toán 11 tập 2 Kết nối tri thức
Bài 7.13 trang 43 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.12 trang 42 Toán 11 tập 2 Kết nối tri thức
Bài 7.12 trang 42 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.11 trang 42 Toán 11 tập 2 Kết nối tri thức
Bài 7.11 trang 42 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.10 trang 42 Toán 11 tập 2 Kết nối tri thức
Bài 7.10 trang 42 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.40 trang 26 Toán 11 tập 2 Kết nối tri thức
Bài 6.40 trang 26 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.39 trang 26 Toán 11 tập 2 Kết nối tri thức
Bài 6.39 trang 26 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.38 trang 26 Toán 11 tập 2 Kết nối tri thức
Bài 6.38 trang 26 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.37 trang 26 Toán 11 tập 2 Kết nối tri thức
Bài 6.37 trang 26 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.36 trang 26 Toán 11 tập 2 Kết nối tri thức
Bài 6.36 trang 26 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.35 trang 26 Toán 11 tập 2 Kết nối tri thức
Bài 6.35 trang 26 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.34 trang 25 Toán 11 tập 2 Kết nối tri thức
Bài 6.34 trang 25 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.33 trang 25 Toán 11 tập 2 Kết nối tri thức
Bài 6.33 trang 25 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.32 trang 25 Toán 11 tập 2 Kết nối tri thức
Bài 6.32 trang 25 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.31 trang 25 Toán 11 tập 2 Kết nối tri thức
Bài 6.31 trang 25 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.30 trang 25 Toán 11 tập 2 Kết nối tri thức
Bài 6.30 trang 25 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.29 trang 25 Toán 11 tập 2 Kết nối tri thức
Bài 6.29 trang 25 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.28 trang 25 Toán 11 tập 2 Kết nối tri thức
Bài 6.28 trang 25 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.27 trang 25 Toán 11 tập 2 Kết nối tri thức: Quy tắc tính toán với lũy thừa
Bài 6.27 trang 25 Toán 11 tập 2 Kết nối tri thức: Quy tắc tính toán với lũy thừa
-
 Bài 6.26 trang 24 Toán 11 tập 2 Kết nối tri thức
Bài 6.26 trang 24 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.25 trang 24 Toán 11 tập 2 Kết nối tri thức
Bài 6.25 trang 24 Toán 11 tập 2 Kết nối tri thức
-
 Bài 6.24 trang 24 Toán 11 tập 2 Kết nối tri thức: Vận dụng hàm số mũ và logarit giải toán
Bài 6.24 trang 24 Toán 11 tập 2 Kết nối tri thức: Vận dụng hàm số mũ và logarit giải toán


















































