Giải bài 11 trang 42 Toán 11 tập 1 SGK Cánh Diều

Đề bài:

Vẽ đồ thị hàm số y = cosx trên đoạn  rồi xác định số nghiệm của phương trình 3cosx + 2 = 0 trên đoạn đó.

Phân tích và Hướng dẫn giải:

Để tìm số nghiệm của phương trình $3\cos x+2=0$ trên đoạn $[-2\pi ;2\pi ]$ bằng phương pháp đồ thị, chúng ta thực hiện các bước sau:

1. Biến đổi phương trình: Chuyển phương trình về dạng $\cos x=c$, trong đó $c$ là một hằng số.

2. Vẽ đồ thị:

   • Vẽ đồ thị hàm số $y=\cos x$ trên đoạn $[-2\pi ;2\pi ]$.

   • Vẽ đường thẳng ngang $y=c$ (với $c$ là hằng số vừa tìm được).

3. Xác định số nghiệm: Số nghiệm của phương trình chính là số giao điểm của đồ thị hàm số $y=\cos x$ và đường thẳng $y=c$.

Lời giải chi tiết:

Ta có: 3cosx + 2 = 0

⇔ cosx = -2/3.

Đường thẳng y =-2/3 và đồ thị hàm số y = cosx trên đoạn  biểu điẽn như sau:

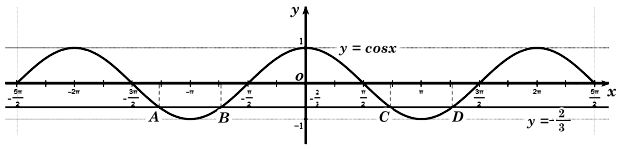
Từ đồ thị, ta thấy đường thẳng y = -2/3 cắt đồ thị hàm số y = cosx trên đoạn  tại 4 điểm A, B, C, D.

Vậy phương trình 3cosx + 2 = 0 có 4 nghiệm trên đoạn