Giải bài 14 trang 42 Toán 11 tập 1 SGK Cánh Diều

Đề bài:

Một cây cầu có dạng cung OA của đồ thị hàm số y = 4,8.sin(x/9) và được mô tả trong hệ trục toạ độ với đơn vị trục là mét như ở Hình 39.

a) Giả sử chiều rộng của con sông là độ dài đoạn thẳng OA. Tìm chiều rộng đó (làm tròn kết quả đến hàng phần mười).

b) Một sà lan chở khối hàng hoá được xếp thành hình hộp chữ nhật với độ cao 3,6 m so với mực nước sông sao cho sà lan có thể đi qua được gầm cầu. Chứng minh rằng chiều rộng của khối hàng hoá đó phải nhỏ hơn 13,1 m.

c) Một sà lan khác cũng chở khối hàng hoá được xếp thành hình hộp chữ nhật với chiều rộng của khối hàng hoá đó là 9 m sao cho sà lan có thể đi qua được gầm cầu. Chứng minh rằng chiều cao của khối hàng hoá đó phải nhỏ hơn 4,3 m.

Phân tích và Hướng dẫn giải:

Để giải bài toán này, chúng ta sẽ thực hiện các bước sau:

• Phần a: Tìm chiều rộng con sông.

  • Chiều rộng con sông chính là độ dài đoạn thẳng $OA$.

  • Các điểm $O$ và $A$ nằm trên trục hoành, nên tại các điểm này, giá trị $y=0$.

  • Ta sẽ giải phương trình 4,8sin(9x​)=0 để tìm hoành độ của $O$ và $A$.

  • Chiều rộng con sông sẽ là hiệu giữa hoành độ của $A$ và hoành độ của $O$.

• Phần b: Chứng minh chiều rộng khối hàng phải nhỏ hơn 13,1 m.

  • Sà lan đi qua gầm cầu, có nghĩa là sà lan phải nằm dưới cung cầu.

  • Độ cao của sà lan là $3,6$ m, tương ứng với giá trị $y=3,6$.

  • Ta sẽ giải phương trình 4,8sin(9x​)=3,6 để tìm các giá trị $x$ tương ứng.

  • Chiều rộng của khối hàng sẽ là hiệu giữa hai giá trị $x$ này.

• Phần c: Chứng minh chiều cao khối hàng phải nhỏ hơn 4,3 m.

  • Sà lan có chiều rộng là $9$ m. Do cây cầu đối xứng qua trục tung của nó, sà lan sẽ có vị trí cân bằng khi cách đều hai bên chân cầu.

  • Tổng chiều rộng cây cầu là $9\pi \approx 28,3$ m. Chiều rộng của sà lan là $9$ m.

  • Ta có thể tìm hoành độ của hai mép sà lan.

  • Thay các hoành độ này vào hàm số $y$ để tìm chiều cao tối đa của cầu tại vị trí đó, chính là chiều cao tối đa mà khối hàng có thể có.

Lời giải chi tiết:

a) Hai vị trí O và A là hai vị trí chân cầu, tại hai vị trí này ta có: y = 0

Quan sát đồ thị ta thấy, đồ thị hàm số y = 4,8.sin(x/9) cắt trục hoành tại điểm O và A liên tiếp nhau với x ≥ 0.

+ Xét k = 0, ta có x₁ = 0;

+ Xét k = 1, ta có x₂ = 9π.

Mà x₁ = 0 nên đây là hoành độ của O, do đó x₂ = 9π là hoành độ của điểm A.

Khi đó OA = 9π ≈ 28,3.

Vậy chiều rộng của con sông xấp xỉ 28,3 m.

b) Do sà lan có độ cao 3,6 m so với mực nước sông nên khi sà lan đi qua gầm cầu thì ứng với y = 3,6.

(Dùng máy tính cầm tay chuyển về chế độ "radian" bấm liên tiếp [SHIFT][sin][3][÷][4] ta được kết quả gần đúng là 0,85)

- Xét k = 0, ta có x₁ ≈ 7,632; x₂ ≈ 20,642.

Ta biểu diễn các giá trị x vừa tìm được trên hệ trục tọa độ vẽ đồ thị hàm số y = 4,8.sin(x/9) như sau: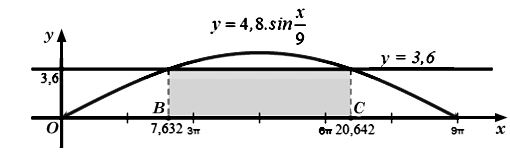

Khi đó để sà lan có thể đi qua được gầm cầu thì khối hàng hóa có độ cao 3,6 m phải có chiều rộng nhỏ hơn độ dài đoạn thẳng BC trên hình vẽ.

Mà BC ≈ 20,642 – 7,632 = 13,01 (m) < 13,1 (m).

Vậy chiều rộng của khối hàng hoá đó phải nhỏ hơn 13,1 m.

c) Giả sử sà lan chở khối hàng được mô tả bởi hình chữ nhật MNPQ:

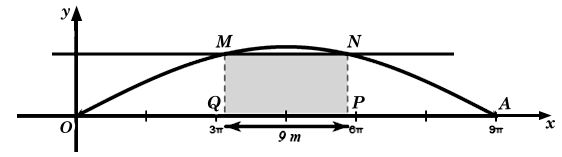
Khi đó QP = 9; OA = 28,3 và OQ = PA.

Mà OQ + QP + PA = OA

⇒ OQ + 9 + OQ ≈ 28,3

⇒ OQ ≈ 9,65

Khi đó:

Vậy để sà lan có thể đi qua được gầm cầu thì chiều cao của khối hàng hoá đó phải nhỏ hơn 4,3 m.