Cách giải và biện luận phương trình Logarit chứa tham số m - Toán 12 chuyên đề
Cách giải và biện luận phương trình logarit có chứa tham số m cũng tương tự như cách giải phương trình mũ chứa tham số đã được giới thiệu trên Hay Học Hỏi.
Cụ thể cách giải phương trình logarit chứa tham số m như thế nào? chúng ta cùng tìm hiểu qua bài viết dưới đây.
» Đừng bỏ lỡ: Các dạng toán bất phương trình mũ, bất phương trình logarit cực hay
Cũng cần lưu ý rằng, phương pháp trình bày dưới đây là phương pháp đồ thị hàm số, thường sử dụng trong các bài toán mà chúng ta thấy không đặt được ẩn phụ để đưa được về dạng pt bậc hai hay bậc nhất hay vận dụng Vi-et để giải theo cách ta hay làm.
• Để giải phương trình logarit chứa tham số m ta cần thực hiện các bước sau:
° Bước 1: Tách m ra khỏi biến số x và đưa về dạng f(x) = T(m)
° Bước 2: Khảo sát sự biến thiên của hàm số f(x) trên D
° Bước 3: Dựa vào bảng biến thiên để xác định giá trị tham số T(m) để đường thẳng y = T(m) nằm ngang (song song Ox) cắt đồ thị hàm số y = f(x).
° Bước 4: Kết luận các giá trị của T(m) để phương trình f(x) = T(m) có nghiệm (hoặc có k nghiệm) trên D.
* Chú ý:
- Nếu hàm số y = f(x) có giá trị lớn nhất và giá trị nhỏ nhất trên D thì giá trị T(m) cần tìm là những m thỏa mãn 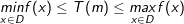
- Nếu bài toán yêu cầu tìm tham số để phương trình có k nghiệm phân biệt, ta chỉ cần dựa vào bảng biến thiên để xác định sao cho đường thẳng y = T(m) nằm ngang cắt đồ thị hàm số y = f(x) tại k điểm phân biệt.
- Khi đặt ẩn số phụ để đổi biến, ta cần đặt điều kiện cho biến mới chính xác, nếu khôngsẽ làm thay đổi kết quả của bài toán do đổi miền giá trị của nó, dẫn đến kết quả sau cùng bị sai.

• Một số bài tập vận dụng giải và biện luận phương trình logarit chứa tham số m
* Bài tập 1: Cho phương trình logarit có tham số m:
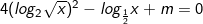
Tìm m để phương trình trên có hai nghiệm phân biệt thuộc khoảng (0;1).
* Lời giải:
- Ta có: 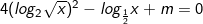
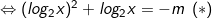
Đặt t = log2x với x ∈ (0,1) thì t<0, khi đó (*) trở thành:
t2 + t = - m (**)
Xét hàm f(t) = t2 + t, với t ∈ (-∞;0) ta có: f'(t) = 2t +1
f'(t) = 0 ⇔ t = -1/2
- Bảng biến thiến thiên: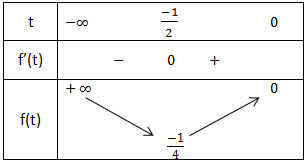
Nhận thấy với mỗi số thực t<0 cho ta một số thực x ∈ (0;1) (vì x = 2t). Do đó để pt(*) có 2 nghiệm phân biệt thì pt(**) phải có 2 nghiệm phân biệt.
Từ bảng biến thiên trên ta thấy để phương trình (**) có 2 nghiệm phân biệt khi và chỉ khi: -1/4 < -m <0 ⇔ 0 < m < 1/4.
* Bài tập 2: Cho phương trình logarit có tham số m sau:
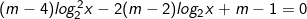 (*)
(*)
Tìm tham số m để phương trình trên có 2 nghiệm thỏa 1 < x1 < 2 < x2.
* Lời giải:
- Đặt t = log2x ⇒ x = 2t (t > 0), khi đó (*) trở thành
(m - 4)t2 - 2(m - 2)t +m - 1 = 0
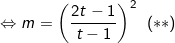 (do t = 1 không phải là nghiệm)
(do t = 1 không phải là nghiệm)
Để pt(*) có 2 nghiệm thỏa 1 < x1 < 2 < x2 thì p(**) phải có hai nghiệm thỏa 0 < t1 < 1 < t2.
Xét hàm số 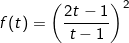 với t ∈ (0;+∞) ta có:
với t ∈ (0;+∞) ta có: 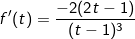
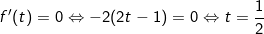
- Bảng biến thiên: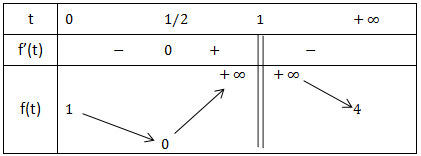
Từ bảng biến thiên ta thấy để pt(**) có 2 nghiệm 0 < t1 < 1 < t2 thì m > 4.
* Bài tập 3: Tìm tham số m để: 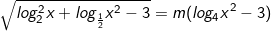 có nghiệm thực thuộc [32;+∞).
có nghiệm thực thuộc [32;+∞).
* Lời giải:
- Ta có: 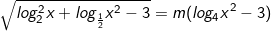
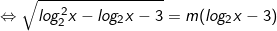 (*)
(*)
Đặt t = log2x, phương trình đã cho trở thành:
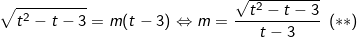
Để pt(*) có nghiệm thực thuộc [32;+∞) thì pt(**) phải có nghiệm t ≥ 5.
Xét hàm số: ![\small f(t)=\frac{\sqrt{t^2-t-3}}{t-3},\: \: t\in [5;+\infty ]](https://hayhochoi.vn/uploads/news/wyswyg/2021_07/1627554405xhtstuml1l.gif) ta có
ta có
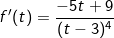 ; Ta thấy
; Ta thấy ![\small f'(t)\leq 0\: \: \forall t\in [5;+\infty ]](https://hayhochoi.vn/uploads/news/wyswyg/2021_07/16275544127vyq19xmyg.gif)
- Bảng biến thiên: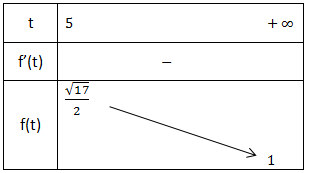
Từ bảng biến thiên ta thấy để pt(*) có nghiệm thực thuộc [32;+∞) thì: 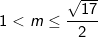
Như vậy, với bài viết về cách giải và biện luận phương trình logarit chứa tham số m ở trên HayHocHoi hy vọng các bạn có thêm phương pháp giải phương trình logarit để vận dụng trong các dạng toán tương tự.
Đánh giá & nhận xét
-
 Bài 7 trang 12 Toán 12 tập 2 Chân trời sáng tạo
Bài 7 trang 12 Toán 12 tập 2 Chân trời sáng tạo
-
 Bài 6 trang 12 Toán 12 tập 2 Chân trời sáng tạo
Bài 6 trang 12 Toán 12 tập 2 Chân trời sáng tạo
-
 Bài 5 trang 12 Toán 12 tập 2 Chân trời sáng tạo
Bài 5 trang 12 Toán 12 tập 2 Chân trời sáng tạo
-
 Bài 4 trang 11 Toán 12 tập 2 Chân trời sáng tạo
Bài 4 trang 11 Toán 12 tập 2 Chân trời sáng tạo
-
 Bài 3 trang 11 Toán 12 tập 2 Chân trời sáng tạo
Bài 3 trang 11 Toán 12 tập 2 Chân trời sáng tạo
-
 Bài 2 trang 11 Toán 12 tập 2 Chân trời sáng tạo
Bài 2 trang 11 Toán 12 tập 2 Chân trời sáng tạo
-
 Bài 1 trang 11 Toán 12 tập 2 Chân trời sáng tạo
Bài 1 trang 11 Toán 12 tập 2 Chân trời sáng tạo
-
 Bài 4.18 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.18 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.17 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.17 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.16 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.16 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.15 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.15 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.14 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.14 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.13 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.13 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.12 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.12 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.11 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.11 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.10 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.10 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.9 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.9 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.8 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.8 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.7 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.7 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.6 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.6 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.5 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.5 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.4 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.4 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.3 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.3 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.2 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.2 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.1 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.1 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 15 trang 83 Toán 12 tập 1 Cánh Diều
Bài 15 trang 83 Toán 12 tập 1 Cánh Diều
-
 Bài 14 trang 83 Toán 12 tập 1 Cánh Diều
Bài 14 trang 83 Toán 12 tập 1 Cánh Diều
-
 Bài 13 trang 83 Toán 12 tập 1 Cánh Diều
Bài 13 trang 83 Toán 12 tập 1 Cánh Diều
-
 Bài 12 trang 83 Toán 12 tập 1 Cánh Diều
Bài 12 trang 83 Toán 12 tập 1 Cánh Diều
-
 Bài 11 trang 83 Toán 12 tập 1 Cánh Diều
Bài 11 trang 83 Toán 12 tập 1 Cánh Diều
-
 Bài 10 trang 82 Toán 12 tập 1 Cánh Diều
Bài 10 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 9 trang 82 Toán 12 tập 1 Cánh Diều
Bài 9 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 8 trang 82 Toán 12 tập 1 Cánh Diều
Bài 8 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 7 trang 82 Toán 12 tập 1 Cánh Diều
Bài 7 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 6 trang 82 Toán 12 tập 1 Cánh Diều
Bài 6 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 5 trang 82 Toán 12 tập 1 Cánh Diều
Bài 5 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 4 trang 82 Toán 12 tập 1 Cánh Diều
Bài 4 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 3 trang 82 Toán 12 tập 1 Cánh Diều
Bài 3 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 2 trang 82 Toán 12 tập 1 Cánh Diều: Tọa Độ Vectơ
Bài 2 trang 82 Toán 12 tập 1 Cánh Diều: Tọa Độ Vectơ


















































