Bài 12 trang 83 Toán 12 tập 1 Cánh Diều

Đề bài:

Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AA' và CC'. Tính góc giữa hai vectơ  và 

Phân tích và Hướng dẫn giải:

1. Biểu diễn Vectơ: Chứng minh $\vec{MN}$ bằng với $\vec{AC}$ (vì $M, N$ là trung điểm và $MN$ song song, bằng $AC$).

2. Xác định Góc: Góc giữa $\vec{MN}$ và $\vec{AD'}$ chính là góc giữa $\vec{AC}$ và $\vec{AD'}$, tức là góc $\widehat{CAD'}$.

3. Kiểm tra Tam giác: Tính độ dài ba cạnh của tam giác $\triangle ACD'$ ($AC, AD', CD'$) để xác định loại tam giác, từ đó suy ra giá trị của góc $\widehat{CAD'}$.

Lời giải chi tiết:

Ta có hình minh họa:

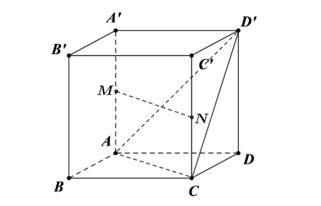
1. Biểu Diễn Vectơ $\vec{MN}$ Theo Vectơ Khác

Vì $M, N$ lần lượt là trung điểm của các cạnh $AA'$ và $CC'$, ta có $MN$ song song và bằng $AC$.

2. Xác Định Góc Giữa $\vec{MN}$ và $\vec{AD'}$

Sử dụng tính chất vectơ bằng nhau, góc giữa hai vectơ $\vec{MN}$ và $\vec{AD'}$ chính là góc giữa $\vec{AC}$ và $\vec{AD'}$:

3. Tính Độ Dài Các Cạnh Của Tam Giác $\triangle ACD'$

Xét tam giác $\triangle ACD'$. Các cạnh của nó là đường chéo của các mặt hình vuông của hình lập phương cạnh $a$:

• $AC$ là đường chéo mặt đáy $ABCD$:

  $$AC = \sqrt{a^2 + a^2} = a\sqrt{2}$$

• $AD'$ là đường chéo mặt bên $ADD'A'$:

  $$AD' = \sqrt{a^2 + a^2} = a\sqrt{2}$$

• $CD'$ là đường chéo mặt bên $CDD'C'$:

  $$CD' = \sqrt{a^2 + a^2} = a\sqrt{2}$$

Do $AD'=AC=CD'=a\sqrt{2}$, nên tam giác $ACD'$ là tam giác đều.

4. Kết Luận Góc Cần Tìm

Vì $\triangle ACD'$ là tam giác đều, góc $\widehat{CAD'}$ là góc trong của nó:

Vậy góc giữa hai vectơ $\vec{MN}$ và $\vec{AD'}$ là: