Bài 12 trang 48 Toán 12 tập 1 Cánh Diều

Đề bài:

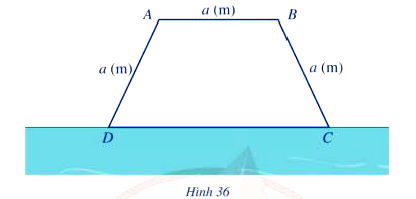
Một bác nông dân có ba tấm lưới thép B40, mỗi tấm dài a (m) và muốn rào một mảnh vườn dọc bờ sông có dạng hình thang cân ABCD như hình 36 (bờ sông là đường thẳng CD không phải rào). Hỏi bác có thể rào được mảnh vườn có diện tích lớn nhát là bao nhiêu mét vuông?

Phân tích và Hướng dẫn giải:

Vì bác nông dân có ba tấm lưới thép, tổng chiều dài lưới thép là $\mathbf{3a}$ ($\text{m}$).

Hàng rào bao gồm ba cạnh $AB, AD, BC$.

Vì $ABCD$ là hình thang cân và $AB$ là cạnh đáy nhỏ (theo hình vẽ và cách đặt tên thường gặp), $AD = BC$ và $AB$ phải được rào bằng một tấm lưới thép ($AB=a$), $AD$ và $BC$ phải được rào bằng hai tấm còn lại ($AD=BC=a$).

Lời giải chi tiết:

Ta kí hiệu như hình sau:

Dựng các đường cao AE và BF của hình thang cân ABCD như hình vẽ trên.

Vì ABCD là hình thang cân nên DE = FC và EF = AB = a.

Đặt DE = FC = x (m) (x > 0). 

a có DC = DE + EF + FC = x + a + x = 2x + a.

Theo định lí Pythagore, ta có:

Rõ ràng, x phải thỏa mãn điều kiện 0 < x < a.

Diện tích của hình thang cân ABCD là: S = (AB + CD)AE 

Xét hàm số  với x ∈ (0; a).

Ta có: 

S'(x) = 0 ⇔ – 2x² – ax + a² = 0

⇔ (x + a)(a – 2x) = 0

⇔ x = – a hoặc x = a/2.

Khi đó trên khoảng (0; a), S'(x) = 0 khi x = a/2.

Bảng biến thiên của hàm số S(x) như sau:

Căn cứ vào bảng biến thiên, ta thấy hàm số S(x) đạt giá trị lớn nhất bằng  tại x = a/2.

Vậy bác đó có thể rào được mảnh vườn có diện tích lớn nhất là  (m²).