Bài 1 trang 42 Toán 12 tập 1 Cánh Diều

Đề bài:

Đồ thị hàm số y = x³ - 3x - 1 là đường cong nào trong các đường cong sau?

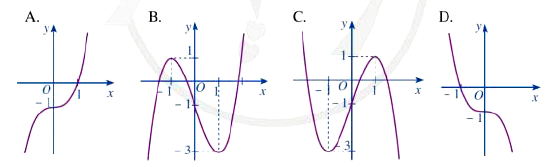
Phân tích và Hướng dẫn giải:

1. Tính đạo hàm: Tìm đạo hàm bậc nhất $y'$ của hàm số.

2. Tìm cực trị: Giải phương trình $y' = 0$ để tìm hoành độ các điểm cực trị.

3. Tính giá trị cực trị: Thay hoành độ vào hàm số $y$ để tìm giá trị cực trị tương ứng ($y_{CT}, y_{CĐ}$).

4. Xây dựng bảng biến thiên: Dựa vào dấu của $y'$ để xác định khoảng tăng, giảm.

5. Nhận dạng đồ thị: Đồ thị đúng phải đi qua các điểm cực trị đã tính và có hình dạng (lên - xuống - lên) khớp với bảng biến thiên.

Lời giải chi tiết:

Đáp án: B

Vì y' =  3x² - 3 = 0 ⇔ x = -1 hoặc x = 1

Lập bảng biến thiên:

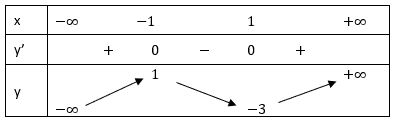
Hàm số đạt cực đại tại x = -1, y_CĐ =  1;

cực tiểu tại x = 1, y_CT = -3 (tâm đối xứng: x = 0, y = -1)

Vậy đồ thị hàm số y = x³ - 3x - 1 là đường cong B