Bài 13 trang 83 Toán 12 tập 1 Cánh Diều

Đề bài:

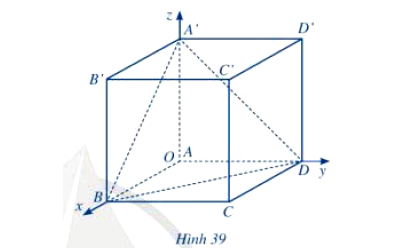
Xét hệ tọa độ Oxyz gắn với hình lập phương ABCD.A'B'C'D' như hình 39, đơn vị của mỗi trục bằng độ dài cạnh hình lập phương. Biết A(0; 0; 0), B(1; 0; 0), D(0; 1; 0), A'(0; 0; 1).

a) Xác định tọa độ các đỉnh còn lại của hình lập phương ABCD.A'B'C'D'.

b) Xác định tọa độ trọng tâm G của tam giác A'BD

c) Xác định tọa độ các vectơ  và . Chứng mih rằng ba điểm O, G, C' thẳng hàng và 

Phân tích và Hướng dẫn giải:

1. Tọa độ Đỉnh (Phần a): Sử dụng tính chất của hình lập phương và các mặt phẳng tọa độ ($A(0; 0; 0) \equiv O$). Cạnh bằng $1$.

   • $C$ là đỉnh đối của $A$ trong mặt phẳng $Oxy$.

   • $B', D', C'$ là các đỉnh trên mặt phẳng $z=1$ (hoặc sử dụng quy tắc hình hộp).

2. Tọa độ Trọng tâm (Phần b): Áp dụng công thức trọng tâm: $x_G = \frac{x_{A'}+x_B+x_D}{3}$.

3. Thẳng hàng (Phần c): Tính $\vec{OG}$ và $\vec{OC'}$. Chứng minh $\vec{OG} = k \cdot \vec{OC'}$, suy ra thẳng hàng và tỉ lệ độ dài.

Lời giải chi tiết:

a) Xác Định Toạ Độ Các Đỉnh Còn Lại

Với $A(0; 0; 0)$, cạnh hình lập phương bằng 1.

• Đỉnh C: $C$ thuộc mặt phẳng $(Oxy)$ nên cao độ $z_C = 0$. Vì $ABCD$ là hình vuông, $C$ có hoành độ bằng $B$ và tung độ bằng $D$.

  $$C(1; 1; 0)$$

• Đỉnh B': $B'$ có cùng $x, y$ với $B$, và cùng $z$ với $A'$.

  $$B'(1; 0; 1)$$

• Đỉnh D': $D'$ có cùng $x, y$ với $D$, và cùng $z$ với $A'$.

  $$D'(0; 1; 1)$$

• Đỉnh C': Áp dụng quy tắc hình hộp $\vec{AC'} = \vec{AA'} + \vec{AB} + \vec{AD}$.

  Ta có:

  $$\vec{AA'}=(0;0;1)$$
  $$\vec{AB}=(1;0;0)$$
  $$\vec{AD}=(0;1;0)$$
  $$\vec{AC'} = (0+1+0; 0+0+1; 1+0+0) = (1;1;1)$$

  Do $A \equiv O$, nên $\vec{OC'} = \vec{AC'} = (1;1;1)$.

  $$\text{Tọa độ } C' \text{ là } C'(1; 1; 1)$$

b) Xác Định Tọa Độ Trọng Tâm $G$ của $\triangle A'BD$

Gọi toạ độ trọng tâm $G$ của tam giác $A'BD$ là $(x_G; y_G; z_G)$.

c) Chứng Minh $O, G, C'$ Thẳng Hàng và $OG = \frac{1}{3}OC'$

Xác định toạ độ các vectơ:

• Vì $O \equiv A(0; 0; 0)$ và $G\left(\frac{1}{3};\frac{1}{3};\frac{1}{3}\right)$ nên:

  $$\vec{OG}=\left(\frac{1}{3};\frac{1}{3};\frac{1}{3}\right)$$

• Vì $O \equiv A(0; 0; 0)$ và $C'(1; 1; 1)$ nên:

  $$\vec{OC'}=(1;1;1)$$

Từ tọa độ hai vectơ, ta thấy mối liên hệ:

Mối quan hệ $\vec{OG}=k\vec{OC'}$ ($k=\frac{1}{3}$) chứng tỏ hai vectơ $\vec{OG}$ và $\vec{OC'}$ cùng phương. Do đó, hai đường thẳng $OG$ và $OC'$ song song hoặc trùng nhau.

Vì $O$ là điểm chung ($OG \cap OC' = O$), nên hai đường thẳng này trùng nhau, tức là ba điểm $O, G, C'$ thẳng hàng.

Từ $\vec{OG}=\frac{1}{3}\vec{OC'}$, lấy độ dài hai vế: