Bài 13 trang 48 Toán 12 tập 1 Cánh Diều

Đề bài:

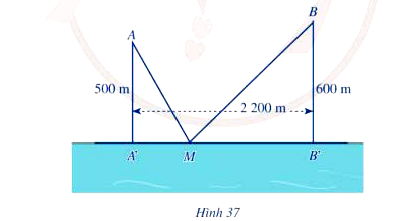
Có hai xã A, B cùng ở một bên bờ sông Lam, khoảng cách từ hai xã đó đến bờ sông lần lượt là AA' = 500 m và BB' = 600 m và người ta đo được A'B' = 2 200 m (Hình 37). Các kĩ sư muốn xây một tramgj cung cấp nước sạch nằm bên bờ sông Lam cho người dân hai xã. Để tiết kiêm chi phí, các kĩ sư cần phải chọn vị trí M của trạm cung cấp nước sạch đó trên đoạn A'B' sao cho tổng khoảng cách từ hai xã đến vị trí M là nhỏ nhất. Hãy tìm giá trị nhỏ nhất của tổng khoảng cách đó.

Phân tích và Hướng dẫn giải:

1. Thiết lập hàm mục tiêu $D(x)$: Đặt $\mathbf{x = A'M}$. Khi đó $\mathbf{B'M = 2\ 200 - x}$. Ta áp dụng định lí Pythagore cho hai tam giác vuông $\triangle AA'M$ và $\triangle BB'M$ để tính $AM$ và $BM$, từ đó thiết lập hàm tổng khoảng cách $\mathbf{D(x) = AM + BM}$.

2. Tìm GTNN: Tính đạo hàm $\mathbf{D'(x)}$ và giải phương trình $\mathbf{D'(x) = 0}$ để tìm điểm cực trị $x_0 \in (0; 2\ 200)$.

3. So sánh: Tính giá trị $D(x)$ tại $x_0$ và tại hai mút.

Lời giải chi tiết:

Đặt A'M = x (m).

Suy ra B'M = A'B' – A'M = 2 200 – x (m).

Rõ ràng, x phải thỏa mãn điều kiện 0 < x < 2 200.

Áp dụng định lí Pythagore ta tính được:

Tổng khoảng cách từ hai vị trí A, B đến vị trí M là:

Xét hàm số:  với x ∈ (0; 2 200).

Ta có:

Trên khoảng (0; 2 200), ta thấy D'(x) = 0 khi x = 1 000.

Bảng biến thiên của hàm số D(x) như sau:

Căn cứ vào bảng biến thiên, ta thấy hàm số D(x) đạt giá trị nhỏ nhất bằng 1100√5 tại x = 1 000.

Vậy giá trị nhỏ nhất của tổng khoảng cách cần tìm là 1100√5 m.