Bài 4 trang 46 Toán 12 tập 1 Cánh Diều

Đề bài:

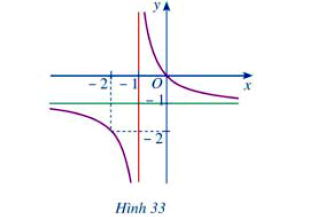
Đường cong ở Hinh 33 là đồ thị của hàm số nào sau đây?

A. 

B. 

C. 

D. 

Phân tích và Hướng dẫn giải:

1. Tiệm cận đứng (TCĐ): Đường thẳng $\mathbf{x = x_0}$ là TCĐ, với $\mathbf{x_0}$ là nghiệm của mẫu số.

2. Tiệm cận ngang (TCN): Đường thẳng $\mathbf{y = a/c}$ là TCN, với $a, c$ là hệ số của $x$ ở tử và mẫu.

3. Điểm đi qua: Kiểm tra giao điểm với trục tung $\mathbf{y(0)}$.

Lời giải chi tiết:

Đáp án: D. 

Từ hình 33, ta thấy:

Đồ thị có tiệm cận đứng x = -1;

tiệm cận ngang y = -1;

đi qua điểm x = 0; y = 0 và điểm x = -2; y = -2.

Nên chỉ có hàm số  thỏa,

Nên đáp án là D