Bài 1 trang 45 Toán 12 tập 1 Cánh Diều

Đề bài:

Cho hàm số y = f(x) có đạo hàm trên R và hàm số y = f'(x) có đồ thị như Hình 31.

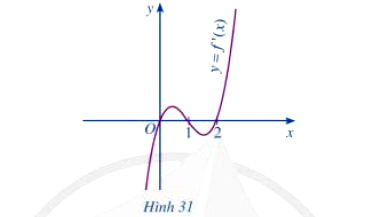
Hàm số f(x) đồng biến trên khoảng:

A. (-∞; 0)

B. (0; 1)

C. (0; 2)

D. (1; 2)

Phân tích và Hướng dẫn giải:

1. Quy tắc: Hàm số $y = f(x)$ đồng biến khi $\mathbf{f'(x) > 0}$.

2. Đồ thị: Trên đồ thị $y = f'(x)$, điều kiện $\mathbf{f'(x) > 0}$ tương ứng với các khoảng mà đồ thị nằm phía trên trục hoành $\mathbf{Ox}$.

3. Xác định khoảng: Quan sát đồ thị $y = f'(x)$ để tìm các khoảng giá trị của $x$ mà đồ thị nằm trên trục $Ox$.

Lời giải chi tiết:

Đáp án: B. (0; 1)

Từ đồ thị ta thấy trên các khoảng (0; 1) và (2; + ∞), đồ thị hàm số y = f'(x) nằm phía trên trục Ox, tức là f'(x) > 0 với mọi x ∈ (0; 1) ∪ (2; + ∞).

Vậy hàm số y = f(x) đồng biến trên mỗi khoảng (0; 1) và (2; + ∞).