Bài 8 trang 73 Toán 12 tập 1 Cánh Diều

Đề bài:

Trong không gian với hệ tọa độ Oxyz, cho hình hộp ABCD.A'B'C'D' có A(4; 6; -5), B(5; 7; -4), C(5; 6; -4), D'(2; 0; 2). Tìm tọa độ các đỉnh còn lại của hình hộp ABCD.A'B'C'D'.

Phân tích và Hướng dẫn giải:

1. Tìm tọa độ đỉnh $D$:

   • Sử dụng tính chất của hình bình hành ở mặt đáy $\mathbf{ABCD}$: $\vec{AB} = \vec{DC}$.

   • Tính $\vec{AB}$.

   • Thiết lập và giải hệ phương trình từ $\vec{AB} = \vec{DC}$ để tìm $D(x_D; y_D; z_D)$.

2. Tìm tọa độ các đỉnh $A', B', C'$:

   • Sử dụng tính chất của hình hộp: các vectơ cạnh bên bằng nhau, ví dụ: $\vec{AA'} = \vec{BB'} = \vec{CC'} = \vec{DD'}$.

   • Tính vectơ cạnh bên $\vec{DD'}$ (vì đã biết $D$ và $D'$).

   • Thiết lập và giải hệ phương trình từ $\vec{AA'} = \vec{DD'}$, $\vec{BB'} = \vec{DD'}$ và $\vec{CC'} = \vec{DD'}$ để tìm $A', B', C'$.

Lời giải chi tiết:

Ta có hình minh họa như sau:

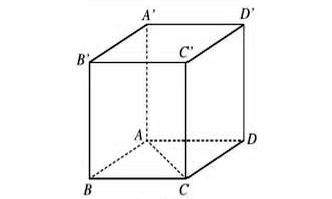
1. Tìm Tọa Độ Đỉnh D

Sử dụng tính chất hình bình hành $ABCD$ có $\vec{AB}=\vec{DC}$.

Ta có vectơ $\vec{AB} = (5 – 4; 7 – 6; – 4 – (– 5)) = (1; 1; 1)$.

Gọi tọa độ của điểm $D$ là $(x_D; y_D; z_D)$, ta có $\vec{DC} = (5 – x_D; 6 – y_D; – 4 – z_D)$.

Vì $\vec{AB}=\vec{DC}$, suy ra:

Tọa độ đỉnh $D$ là $D(4; 5; – 5)$.

2. Tìm Tọa Độ Các Đỉnh A', B', C'

Sử dụng tính chất của hình hộp: các vectơ cạnh bên song song và bằng nhau, tức là $\vec{AA'} = \vec{BB'} = \vec{CC'} = \vec{DD'}$.

Ta tính vectơ $\vec{DD'} = (2 – 4; 0 – 5; 2 – (– 5)) = (– 2; – 5; 7)$.

2.1. Tìm Tọa Độ A'

Ta có $\vec{AA'}=\vec{DD'}$. Gọi $A'(x_{A'}; y_{A'}; z_{A'})$, với $\vec{AA'} = (x_{A'} – 4; y_{A'} – 6; z_{A'} + 5)$.

Tọa độ đỉnh $A'$ là $A'(2; 1; 2)$.

2.2. Tìm Tọa Độ B'

Ta có $\vec{BB'}=\vec{DD'}$. Gọi $B'(x_{B'}; y_{B'}; z_{B'})$, với $\vec{BB'} = (x_{B'} – 5; y_{B'} – 7; z_{B'} + 4)$.

Tọa độ đỉnh $B'$ là $B'(3; 2; 3)$.

2.3. Tìm Tọa Độ C'

Ta có $\vec{CC'}=\vec{DD'}$. Gọi $C'(x_{C'}; y_{C'}; z_{C'})$, với $\vec{CC'} = (x_{C'} – 5; y_{C'} – 6; z_{C'} + 4)$.

Tọa độ đỉnh $C'$ là $C'(3; 1; 3)$.