Bài 14 trang 96 Toán 10 tập 2 Kết nối tri thức

Bài 14 trang 96 Toán 10 Tập 2 Kết nối tri thức:

Cho hình vuông ABCD có cạnh bằng a. Gọi M, N tương ứng là trung điểm của các cạnh AB, BC.

a) Biểu thị các vectơ $\overrightarrow{DM},\overrightarrow{AN}$ theo các vectơ $\overrightarrow{AB},\: \overrightarrow{AD}$ 

b) Tính $\overrightarrow{DM}.\: \overrightarrow{AN}$ và tìm góc giữa hai đường thẳng DM và AN.

Phân Tích và Hướng Dẫn Giải:

1. Biểu thị Vectơ (a): Sử dụng quy tắc hiệu ($\overrightarrow{DM} = \overrightarrow{AM} - \overrightarrow{AD}$) và quy tắc cộng ($\overrightarrow{AN} = \overrightarrow{AB} + \overrightarrow{BN}$).

2. Tính Tích Vô hướng (b): Áp dụng công thức $\overrightarrow{u} \cdot \overrightarrow{v} = |\overrightarrow{u}| |\overrightarrow{v}| \cos(\theta)$ hoặc $\overrightarrow{u} \cdot \overrightarrow{v} = u_1 v_1 + u_2 v_2$. Do hình học là hình vuông, ta có $AB = AD = a$ và $\overrightarrow{AB} \cdot \overrightarrow{AD} = 0$.

3. Tìm Góc: Nếu $\overrightarrow{DM} \cdot \overrightarrow{AN} = 0$, thì $\overrightarrow{DM} \perp \overrightarrow{AN}$, và góc giữa hai đường thẳng bằng $90^\circ$.

Giải bài 14 trang 96 Toán 10 Tập 2 Kết nối tri thức:

Ta có hình minh họa như sau:

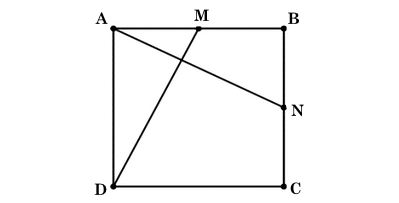
a) Vì M là trung điểm của AB nên $\overrightarrow{AM}=\frac{1}{2}\overrightarrow{AB}$

Vì vậy, ta có: $\overrightarrow{DM}=\overrightarrow{AM}-\overrightarrow{AD}=\frac{1}{2}\overrightarrow{AB}-\overrightarrow{AD}$

Vì N là trung điểm của BC nên $\overrightarrow{BN}=\frac{1}{2}\overrightarrow{BC}$ 

Vì ABCD là hình vuông nên $\overrightarrow{BC}=\overrightarrow{AD}$

Khi đó, $\overrightarrow{BN}=\frac{1}{2}\overrightarrow{AD}$

Theo quy tắc ba điểm ta có: 

$\overrightarrow{AN}=\overrightarrow{AB}+\overrightarrow{BN}=\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}$

b) Vì ABCD là hình vuông nên ta có: AB = AD = a

Vì AB ⊥ AD nên: $\overrightarrow{AB}.\overrightarrow{AD}=0$ 

Từ đó, ta có:

$\overrightarrow{DM}.\overrightarrow{AN}=\left ( \frac{1}{2}\overrightarrow{AB}-\overrightarrow{AD} \right ).\left ( \overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD} \right )$

$=\frac{1}{2}(\overrightarrow{AB})^2+\frac{1}{4}\overrightarrow{AB}.\overrightarrow{AD}-\overrightarrow{AD}.\overrightarrow{AB}-\frac{1}{2}(\overrightarrow{AD})^2$

$=\frac{1}{2}AB^2+\frac{1}{4}.0-0-\frac{1}{2}AD^2$

$=\frac{1}{2}(AB^2-AD^2)=0$

Vi vậy: $\overrightarrow{DM}.\overrightarrow{AN}=0\Leftrightarrow \overrightarrow{DM}\perp \overrightarrow{AN}$

⇔ DM ⊥ AN

Vậy góc giữa hai đường thẳng DM và AN bằng 90°.