Bài 6.30 trang 28 Toán 10 tập 2 Kết nối tri thức
Bài tập 6.30, trang 28 SGK Toán 10 Tập 2 (Kết nối tri thức), là bài tập tổng hợp về khảo sát và vẽ đồ thị hàm số bậc hai ($\mathbf{y = ax^2 + bx + c}$). Đối với mỗi hàm số, ta cần xác định đồ thị (Parabol), tập giá trị, và các khoảng đồng biến/nghịch biến dựa trên toạ độ đỉnh.
Bài 6.30 trang 28 Toán 10 Tập 2 Kết nối tri thức:
Với mỗi hàm số dưới đây, hãy vẽ đồ thị, tìm tập giá trị, khoảng đồng biến, khoảng nghịch biến của nó:
a) y = – x2 + 6x – 9;
b) y = – x2 – 4x + 1;
c) y = x2 + 4x;
d) y = 2x2 + 2x + 1.
Phân tích Phương pháp Khảo sát Parabol
-
Hướng Parabol: Dựa vào dấu của $a$ ($a>0$ quay lên, $a<0$ quay xuống).
-
Tọa độ Đỉnh $I$: $x_I = -\frac{b}{2a}$, $y_I = y(x_I)$.
-
Trục đối xứng: $x = x_I$.
-
Tập Giá trị: Nếu $a>0$, TXG là $[y_I; +\infty)$. Nếu $a<0$, TXG là $(-\infty; y_I]$.
-
Tính Đơn điệu: Hàm số đồng/nghịch biến trên các khoảng $(-\infty; x_I)$ và $(x_I; +\infty)$, ngược chiều với hướng quay của Parabol.
Giải bài 6.30 trang 28 Toán 10 Tập 2 Kết nối tri thức:
a) y = – x2 + 6x – 9 là hàm số bậc hai nên đồ thị là một parabol.
Hệ số a = – 1 < 0 nên bề lõm của đồ thị quay xuống dưới.
Parabol trên có:
- Tọa độ đỉnh I(3; 0);
- Trục đối xứng x = 3;
- Cắt trục Oy tại điểm A(0; – 9);
- Điểm đối xứng với A qua trục đối xứng x = 3 là B(6; – 9);
- Lấy điểm D(1; – 4) thuộc parabol, điểm đối xứng với D là trục đối xứng x = 3 là E(5; – 4).
Vẽ đường cong đi qua các điểm trên ta được đồ thị hàm số cần vẽ.
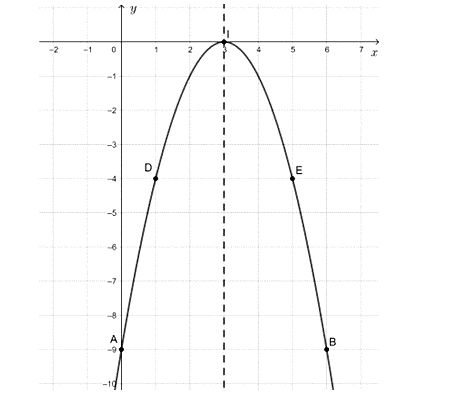
Từ đồ thị ta thấy:
- Tập giá trị của hàm số là (– ∞; 0].
- Hàm số đồng biến trên khoảng (– ∞; 3) (do đồ thị hàm số đi lên từ trái sang phải) và nghịch biến trên khoảng (3; + ∞) (do đồ thị hàm số đi xuống từ trái sang phải).
b) y = – x2 – 4x + 1 là hàm số bậc hai nên đồ thị là một parabol.
Hệ số a = – 1 < 0 nên bề lõm của đồ thị quay xuống dưới.
Parabol trên có:
- Tọa độ đỉnh I(– 2; 5);
- Trục đối xứng x = – 2;
- Cắt trục Oy tại điểm A(0; 1);
- Điểm đối xứng với A qua trục đối xứng x = – 2 là B(– 4; 1);
- Lấy điểm C(– 1; 4) thuộc đồ thị, điểm đối xứng với C qua trục đối xứng x = – 2 là D(– 3; 4).
Vẽ đường cong đi qua các điểm trên ta được đồ thị hàm số cần vẽ.
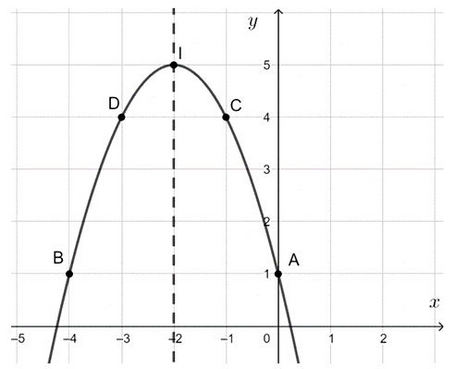
Từ đồ thị hàm số ta thấy:
- Tập giá trị của hàm số là (– ∞; 5].
- Hàm số đồng biến trên khoảng (– ∞; – 2) và nghịch biến trên khoảng (– 2; + ∞).
c) y = x2 + 4x là hàm số bậc hai nên đồ thị là một parabol.
Hệ số a = 1 > 0 nên bề lõm của đồ thị quay lên trên.
Parabol trên có:
- Tọa độ đỉnh I(– 2; – 4);
- Trục đối xứng x = – 2;
- Cắt trục Oy tại điểm gốc tọa độ O(0; 0);
- Điểm đối xứng với O qua trục đối xứng x = – 2 là điểm B(– 4; 0);
- Lấy điểm C(– 1; – 3) thuộc đồ thị, điểm đối xứng với C qua trục đối xứng x = – 2 là D(– 3; – 3).
Vẽ đường cong đi qua các điểm trên ta được đồ thị cần vẽ.
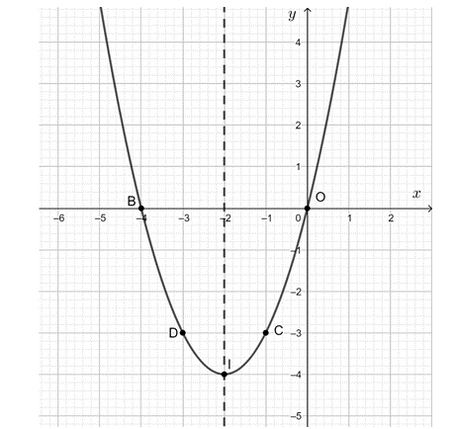
Từ đồ thị hàm số ta thấy:
- Tập giá trị của hàm số là [– 4; + ∞).
- Hàm số nghịch biến trên khoảng (– ∞; – 2) và đồng biến trên khoảng (– 2; + ∞).
d) y = 2x2 + 2x + 1 là hàm số bậc hai nên đồ thị là một parabol.
Hệ số a = 2 > 0 nên bề lõm của đồ thị quay lên trên.
Parabol trên có:
- Tọa độ đỉnh I $\left ( -\frac{1}{2};\frac{1}{2} \right )$
- Trục đối xứng x = 1/2
- Cắt trục Oy tại điểm A(0; 1).
- Điểm đối xứng với A qua trục đối xứng $x=-\frac{1}{2}$ là B(– 1; 1);
- Lấy điểm C(1; 5) thuộc đồ thị, điểm đối xứng với C qua trục đối xứng x = -1/2 là D(– 2; 5).
Vẽ đường cong đi qua các điểm đã cho ta được đồ thị cần vẽ.
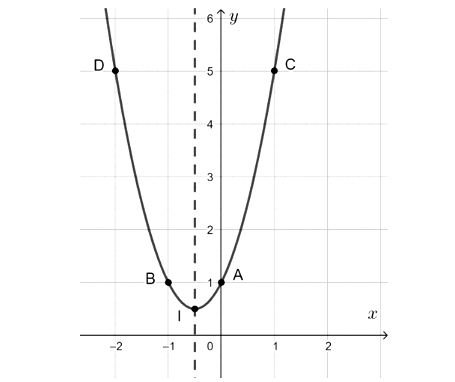
Từ đồ thị ta thấy:
- Tập giá trị của hàm số là $\left [\frac{1}{2};+\infty \right )$
- Hàm số nghịch biến trên khoảng $\left (-\infty ;-\frac{1}{2} \right )$ và đồng biến trên khoảng $\left (\frac{1}{2};+\infty \right )$
Tóm lại, việc khảo sát Parabol $y = ax^2 + bx + c$ được tóm tắt qua bảng sau:
| Hàm số | a | Đỉnh I(xI;yI) | Tập Giá trị | ĐB/NB (Tính đơn điệu) |
| a) $–x^2+6x–9$ | $a<0$ | $I(3; 0)$ | $(– \infty; 0]$ | ĐB $(–\infty; 3)$, NB $(3; +\infty)$ |
| b) $–x^2–4x+1$ | $a<0$ | $I(-2; 5)$ | $(– \infty; 5]$ | ĐB $(–\infty; -2)$, NB $(-2; +\infty)$ |
| c) $x^2+4x$ | $a>0$ | $I(-2; -4)$ | $[-4; +\infty)$ | NB $(–\infty; -2)$, ĐB $(-2; +\infty)$ |
| d) $2x^2+2x+1$ | $a>0$ | $I(-\frac{1}{2}; \frac{1}{2})$ | $[\frac{1}{2}; +\infty)$ | NB $(–\infty; -\frac{1}{2})$, ĐB $(-\frac{1}{2}; +\infty)$ |
• Xem thêm:
Đánh giá & nhận xét
-
 Bài 7.12 trang 41 Toán 10 tập 2 Kết nối tri thức
Bài 7.12 trang 41 Toán 10 tập 2 Kết nối tri thức
-
 Bài 7.11 trang 41 Toán 10 tập 2 Kết nối tri thức
Bài 7.11 trang 41 Toán 10 tập 2 Kết nối tri thức
-
 Bài 7.10 trang 41 Toán 10 tập 2 Kết nối tri thức
Bài 7.10 trang 41 Toán 10 tập 2 Kết nối tri thức
-
 Bài 7.9 trang 41 Toán 10 tập 2 Kết nối tri thức
Bài 7.9 trang 41 Toán 10 tập 2 Kết nối tri thức
-
 Bài 7.8 trang 41 Toán 10 tập 2 Kết nối tri thức
Bài 7.8 trang 41 Toán 10 tập 2 Kết nối tri thức
-
 Bài 7.7 trang 41 Toán 10 tập 2 Kết nối tri thức
Bài 7.7 trang 41 Toán 10 tập 2 Kết nối tri thức
-
 Bài 7.34 trang 58 Toán 10 tập 2 Kết nối tri thức
Bài 7.34 trang 58 Toán 10 tập 2 Kết nối tri thức
-
 Bài 7.33 trang 58 Toán 10 tập 2 Kết nối tri thức
Bài 7.33 trang 58 Toán 10 tập 2 Kết nối tri thức
-
 Bài 7.32 trang 58 Toán 10 tập 2 Kết nối tri thức
Bài 7.32 trang 58 Toán 10 tập 2 Kết nối tri thức
-
 Bài 7.31 trang 58 Toán 10 tập 2 Kết nối tri thức
Bài 7.31 trang 58 Toán 10 tập 2 Kết nối tri thức
-
 Bài 7.30 trang 58 Toán 10 tập 2 Kết nối tri thức
Bài 7.30 trang 58 Toán 10 tập 2 Kết nối tri thức
-
 Bài 7.29 trang 58 Toán 10 tập 2 Kết nối tri thức
Bài 7.29 trang 58 Toán 10 tập 2 Kết nối tri thức
-
 Bài 7.28 trang 58 Toán 10 tập 2 Kết nối tri thức
Bài 7.28 trang 58 Toán 10 tập 2 Kết nối tri thức
-
 Bài 7.27 trang 58 Toán 10 tập 2 Kết nối tri thức
Bài 7.27 trang 58 Toán 10 tập 2 Kết nối tri thức
-
 Bài 7.26 trang 58 Toán 10 tập 2 Kết nối tri thức
Bài 7.26 trang 58 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6.34 trang 29 Toán 10 tập 2 Kết nối tri thức
Bài 6.34 trang 29 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6.33 trang 29 Toán 10 tập 2 Kết nối tri thức
Bài 6.33 trang 29 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6.32 trang 28 Toán 10 tập 2 Kết nối tri thức
Bài 6.32 trang 28 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6.31 trang 28 Toán 10 tập 2 Kết nối tri thức
Bài 6.31 trang 28 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6.29 trang 28 Toán 10 tập 2 Kết nối tri thức
Bài 6.29 trang 28 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6.28 trang 28 Toán 10 tập 2 Kết nối tri thức
Bài 6.28 trang 28 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6.27 trang 28 Toán 10 tập 2 Kết nối tri thức
Bài 6.27 trang 28 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6.26 trang 28 Toán 10 tập 2 Kết nối tri thức: Tính đơn điệu hàm số bậc 2
Bài 6.26 trang 28 Toán 10 tập 2 Kết nối tri thức: Tính đơn điệu hàm số bậc 2
-
 Bài 6.25 trang 28 Toán 10 tập 2 Kết nối tri thức
Bài 6.25 trang 28 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6.24 trang 28 Toán 10 tập 2 Kết nối tri thức
Bài 6.24 trang 28 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6.23 trang 27 Toán 10 tập 2 Kết nối tri thức
Bài 6.23 trang 27 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6.22 trang 27 Toán 10 tập 2 Kết nối tri thức
Bài 6.22 trang 27 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6.21 trang 27 Toán 10 tập 2 Kết nối tri thức
Bài 6.21 trang 27 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6.20 trang 27 Toán 10 tập 2 Kết nối tri thức
Bài 6.20 trang 27 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6.19 trang 24 Toán 10 tập 2 Kết nối tri thức: Bất phương trình bậc 2
Bài 6.19 trang 24 Toán 10 tập 2 Kết nối tri thức: Bất phương trình bậc 2
-
 Bài 6.18 trang 24 Toán 10 tập 2 Kết nối tri thức
Bài 6.18 trang 24 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6.17 trang 24 Toán 10 tập 2 Kết nối tri thức
Bài 6.17 trang 24 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6.16 trang 24 Toán 10 tập 2 Kết nối tri thức
Bài 6.16 trang 24 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6.15 trang 24 Toán 10 tập 2 Kết nối tri thức
Bài 6.15 trang 24 Toán 10 tập 2 Kết nối tri thức
-
 Bài 16 trang 96 Toán 10 tập 2 Kết nối tri thức
Bài 16 trang 96 Toán 10 tập 2 Kết nối tri thức
-
 Bài 15 trang 96 Toán 10 tập 2 Kết nối tri thức
Bài 15 trang 96 Toán 10 tập 2 Kết nối tri thức
-
 Bài 14 trang 96 Toán 10 tập 2 Kết nối tri thức
Bài 14 trang 96 Toán 10 tập 2 Kết nối tri thức
-
 Bài 13 trang 96 Toán 10 tập 2 Kết nối tri thức
Bài 13 trang 96 Toán 10 tập 2 Kết nối tri thức
-
 Bài 12 trang 96 Toán 10 tập 2 Kết nối tri thức
Bài 12 trang 96 Toán 10 tập 2 Kết nối tri thức


















































