Bài 6.22 trang 27 Toán 10 tập 2 Kết nối tri thức

Bài 6.22 trang 27 Toán 10 Tập 2 Kết nối tri thức:

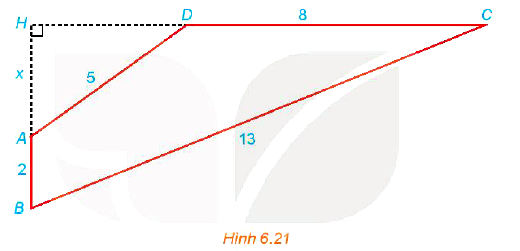
Cho tứ giác ABCD có AB ⊥ CD; AB = 2; BC = 13; CD = 8; DA = 5 (H.6.21). Gọi H là giao điểm của AB và CD và đặt x = AH. Hãy thiết lập một phương trình để tính độ dài x, từ đó tính diện tích tứ giác ABCD. 

Phân tích Phương pháp Giải

1. Biểu diễn các đoạn thẳng: Biểu diễn $HD$, $HC$, $HB$ theo ẩn $x$ (và các giả thiết Pitago).

2. Lập Phương trình: Áp dụng Định lý Pitago cho $\triangle HBC$ vuông tại $H$: $\mathbf{HB^2 + HC^2 = BC^2}$.

3. Giải PT chứa căn: Giải phương trình chứa căn bậc hai tìm $x$.

4. Tính Diện tích: Diện tích tứ giác $ABCD$ là hiệu của hai diện tích tam giác vuông: $\mathbf{S_{ABCD} = S_{\triangle HBC} - S_{\triangle HAD}}$.

Giải bài 6.22 trang 27 Toán 10 Tập 2 Kết nối tri thức:

Đặt AH = x, x > 0. 

Xét tam giác AHD vuông tại H, theo định lí Pythagore ta có: 

AD² = AH² + HD² ⇔ HD² = AD² – AH² = 5² – x² = 25 – x² 

$\Rightarrow HD=\sqrt{25-x^2}$

Ta có $HC=HD+DC$ $=\sqrt{25-x^2}+8$

HB = AH + AB = x + 2 

Xét tam giác HBC vuông tại H, theo định lí Pythagore ta có: 

BC² = HB² + HC² 

$\Leftrightarrow 13^2=(x+2)^2+(\sqrt{25-x^2}+8)^2$

⇔ x² + 4x + 4 + 25 – x² + 16$\sqrt{25-x^2}$ + 64 – 169 = 0

⇔ 16$\sqrt{25-x^2}$ = – 4x + 76 

⇔ 4$\sqrt{25-x^2}$ = – x + 19  (*) 

Ta giải phương trình (*) để tìm x:

Bình phương hai vế của phương trình (*) ta được: 

16.(25 – x²) = x² – 38x + 361

⇔ 17x² – 38x – 39 = 0  

⇔ x = 3 hoặc x = -13/17

Thay lần lượt các giá trị trên vào phương trình (1), ta thấy hai giá trị x = 3 và x = -13/17 đều thỏa mãn. 

Vì điều kiện của x là x > 0 nên ta chọn x = 3.

Nên ta tính được AH = 3. 

Suy ra: HD = 4

HC = 4 + 8 = 12

HB = 3 + 2 = 5

Diện tích tam giác HAD là S₁ = $\frac{1}{2}$HA . HD = $\frac{1}{2}$. 3 . 4 = 6. 

Diện tích tam giác HBC là S₂ = $\frac{1}{2}$HB . HC = $\frac{1}{2}$. 5 . 12 = 30.

Vậy diện tích tứ giác ABCD là S = S₂ – S₁ = 30 – 6 = 24.