Bài 4.14 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.14 SGK Toán 12 Tập 2 Kết nối tri thức là bài tập ứng dụng tích phân xác định để tính diện tích hình phẳng giới hạn bởi hai đồ thị hàm số y=f(x) và y=g(x), trên một đoạn xác định.
Bài 4.14 SGK Toán 12Tập 2 Kết nối tri thức:
Tính diện tích của hình phẳng được tô màu trong Hình 4.29.

Phân tích và Hướng dẫn Giải Bài 4.14 (Kết nối tri thức)
Hình phẳng được tô màu giới hạn bởi hai hàm số $f(x) = 5x - x^2$ và $g(x) = x$.
Công thức tính diện tích hình phẳng giới hạn bởi $y=f(x)$ và $y=g(x)$ trên đoạn $[a, b]$ là:
-
Tìm cận $a, b$: Giải phương trình $f(x) = g(x)$ để tìm hoành độ giao điểm, xác định đoạn $[a, b]$.
-
Thiết lập hàm tích phân: $f(x) - g(x) = (5x - x^2) - x = 4x - x^2$.
-
Xét dấu: Kiểm tra dấu của hàm $(4x - x^2)$ trên đoạn $[0, 4]$.
Giải bài 4.14 SGK Toán 12 Tập 2 Kết nối tri thức:
Diện tích cần tính là:
$S=\int_{0}^{4}|5x-x^2-x|dx$ $=\int_{0}^{4}|4x-x^2|dx$
$=\int_{0}^{4}(4x-x^2)dx\left.\begin{matrix}$ $=\left(2x^2-\frac{x^3}{3}\right)\\\end{matrix}\right|_{0}^{4}=\frac{32}{3}$
Tổng kết: Bài 4.14 SGK Toán 12 Tập 2 Kết nối tri thức đã ứng dụng tích phân để tính diện tích hình phẳng.
-
Hàm tích phân là $\mathbf{h(x) = (5x - x^2) - x = 4x - x^2}$.
-
Cận tích phân là các giao điểm: $x = 0$ và $x = 4$.
-
Diện tích hình phẳng được tính là $\mathbf{S = \int_{0}^{4} (4x - x^2) dx = \frac{32}{3}}$.
Việc xác định đúng hàm bên trên và hàm bên dưới là chìa khóa để giải quyết bài toán tính diện tích. Hãy thường xuyên ghé thăm hayhochoi.vn để cập nhật thêm nhiều bài giải và kiến thức toán học bổ ích khác nhé!
» Xem thêm:
Bài 4.11 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.12 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.13 SGK Toán 12 tập 2 Kết nối tri thức
Đánh giá & nhận xét
-
 Bài 4.18 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.18 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.17 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.17 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.16 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.16 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.15 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.15 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.13 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.13 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.12 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.12 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.11 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.11 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.10 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.10 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.9 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.9 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.8 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.8 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.7 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.7 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.6 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.6 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.5 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.5 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.4 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.4 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.3 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.3 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.2 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.2 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.1 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.1 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.35 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.35 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.34 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.34 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.33 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.33 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.32 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.32 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.31 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.31 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.30 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.30 SGK Toán 12 tập 2 Kết nối tri thức
-
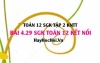 Bài 4.29 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.29 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.28 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.28 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.27 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.27 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.26 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.26 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.25 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.25 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.24 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.24 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.23 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.23 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.22 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.22 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.21 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.21 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.20 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.20 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 6.21 SGK Toán 12 tập 2 Kết nối tri thức
Bài 6.21 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 6.20 SGK Toán 12 tập 2 Kết nối tri thức
Bài 6.20 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 6.19 SGK Toán 12 tập 2 Kết nối tri thức
Bài 6.19 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 6.18 SGK Toán 12 tập 2 Kết nối tri thức
Bài 6.18 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 6.17 SGK Toán 12 tập 2 Kết nối tri thức
Bài 6.17 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 6.16 SGK Toán 12 tập 2 Kết nối tri thức
Bài 6.16 SGK Toán 12 tập 2 Kết nối tri thức


















































