Tìm m để hàm số có cực đại, cực tiểu (xác định m để hàm số có cực trị) - Toán 12 chuyên đề

Vậy cách tìm m để hàm số có cực trị (cực đại, cực tiểu) (hay xác định m để hàm số có cực trị) như thế nào? chúng ta cùng đi tìm hiều qua bài viết dưới đây.

I. Phương pháp chung để tìm cực trị (cực đại, cực tiểu) của hàm số

• Để thực hiện các yêu cầu về điều kiện có cực trị của hàm số y=f(x) ta thực hiện theo các bước:

- Bước 1: Tìm miền xác định D.

- Bước 2: Tính đạo hàm y'.

- Bước 3: Lựa chọn theo một trong 2 cách sau:

+) Cách 1: Nếu xét được dấu của y' thì:

 Hàm số có k cực trị ⇔ Phương trình y'=0 có k nghiệm phân biệt và y' đổi dấu qua các nghiệm đó.

+) Cách 2: Nếu không xét được dấu của y' hoặc bài toán yêu cầu cụ thể về cực đại hoặc cực tiểu thì ta tính thêm y''. Khi đó:

i) Hàm số có cực trị ⇔ Hệ sau có nghiệm thuộc D: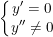 

ii) Hàm số có cực tiểu ⇔ Hệ sau có nghiệm thuộc D: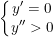 

iii) Hàm số có cực đại ⇔ Hệ sau có nghiệm thuộc D: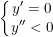 

II. Bài tập, ví dụ minh họa cách tìm m để hàm số có cực đại, cực tiểu (hay xác định m để hàm số có cực trị).

* Bài tập 1: Tìm m để hàm số y = (m - 1)x³ - 3x² - (m + 1)x + 3m² - m + 2 có cực đại và cực tiểu.

* Lời giải:

- TXĐ: D = R

- y' = 3(m - 1)x² - 6x - (m + 1)

Cho y' = 0 ⇔ 3(m - 1)x² - 6x - (m + 1) = 0

Để hàm số có cực đại và cực tiểu thì: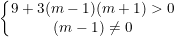

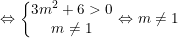
Vậy với m≠1 thì hàm số có cực đại, cực tiểu.

* Bài tập 2: Xác định m để hàm số sau có 3 điểm cực trị: y = mx⁴ - (m + 1) x² + 2m - 1.

* Lời giải:

- TXĐ: D = R

- Ta có: y' = 4mx³ - 2(m + 1)x = 0

 ⇔ x[4mx² - 2(m + 1)] = 0

 ⇔ x = 0 hoặc 2mx² = m + 1

Hàm số có 3 điểm cực trị khi và chỉ khi: 2mx² = m + 1 có 2 nghiệm

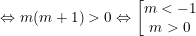
Kết luận: Vậy hàm số có 3 cực trị khi và chỉ khi m<-1 hoặc m>0.

* Bài tập 3: Cho hàm số: y = x³ - 2(m + 1)x² + (m² - 3m + 2)x + 4  (*). Xác định m để hàm số (*) có cực đại và cực tiểu nằm về 2 phía của trục tung.

* Lời giải:

- TXĐ: D = R

- Ta có y' = 3x² - 2(2m + 1)x + m² - 3m + 2

- Hàm số đạt cực đại, cực tiểu nằm về 2 phía của trục tung khi và chỉ khi y' = f'(x) = 0 có hai nghiệm phân biệt x₁, x₂ thỏa mãn x₁ < 0 < x₂ (khi đó c/a của pt bậc 2 trái dấu):

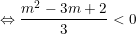
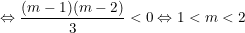
Vậy với 1<m<2 thì hàm số trên có cực đại và cực tiểu nằm về hai phía đối với trục tung.

* Bài tập 4: Cho hàm số   (*)

Tìm α để hàm số có cực đại, cực tiểu thoả: y_CĐ + y_CT = -6.

* Lời giải:

- TXĐ: R\{-1}

- Ta có: 

⇔ x² + 2x + sinα - |sinα| + 1 = 0  (1)

Δ = 4 - 4(sinα - |sinα| + 1) = 4(|sinα| - sinα)

Điều kiện để hàm số có cực đại và cực tiểu là: 

Với Δ > 0 ⇔ |sinα| - sinα > 0

 ⇔ sinα < 0 

 ⇔ (2k + 1)π < α < (k + 1)2π (k ∈ Z) (2)

- Theo bài ra: y_CĐ + y_CT = -6

- Từ (*) khi sinα < 0, ta có:

nên y_CĐ + y_CT = -6:

⇔ 2(x_CĐ + x_CT) + 2sinα = -6

(x_CĐ, x_CT là 2 nghiệm của (1) nên x_CĐ + x_CT = -2)

 ⇔ 2.(-2) + 2sinα = -6 ⇔ sinα = -1

Thoả điều kiện (2), do đó:

 thì hàm số có cực đại, cực tiểu thoả y_CĐ + y_CT = -6.