Bài 14 trang 38 Toán 12 tập 1 Chân trời sáng tạo

Đề bài:

Cho một hình trụ nội tiếp trong hình nón có chiều cao bằng 12 cm và bán kính đáy bằng 5 cm (Hình 4a). Người ta cắt hình nón, trụ này theo mặt phẳng chứa đường thẳng nối đỉnh và tâm hình tròn đáy của hình nón thì thu được một hình phẳng như hình 4b.

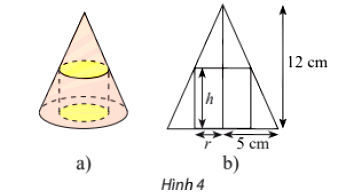
a) Chứng minh rằng công thức tính bán kính r của đáy hình trụ theo chiều cao h của nó là:

b) Chứng minh biểu thức sau biểu thị thể tích khối trụ theo h:

c) Tìm h để khối trụ có thể tích lớn nhất.

Phân tích và Hướng dẫn giải

Để giải bài toán này, chúng ta sẽ thực hiện các bước sau:

• Câu a): Sử dụng kiến thức về định lí Thales trong tam giác đồng dạng để tìm mối liên hệ giữa bán kính , chiều cao $h$ của khối trụ và các kích thước của khối nón.

• Câu b): Dùng công thức thể tích khối trụ  và biểu thức  vừa chứng minh ở câu a) để biểu diễn  theo .

• Câu c): Dùng đạo hàm để tìm giá trị lớn nhất của hàm số thể tích .

  • Tính đạo hàm .

  • Cho  để tìm các điểm cực trị.

  • Lập bảng biến thiên để xác định giá trị lớn nhất của hàm số trong khoảng xác định.

Lời giải chi tiết:

a) Ta có hình vẽ như sau:

Ta có A'O' // AO nên 

Lại có A'C // SO nên 

Từ đó suy ra .

Mà SO = 12 cm, OA = 5 cm, OC = r, SO' = SO – OO' = 12 – h.

Do đó, .

b) Thể tích của khối trụ là V = πr²h

Vậy thể tích khối trụ theo h là

c) Rõ ràng h phải thỏa mãn điều kiện 0 < h < 12.

Xét hàm số  với h ∈ (0; 12).

Ta có 

Trên khoảng (0; 12), ta có V'(h) = 0 khi h = 4.

Bảng biến thiên:

Căn cứ vào bảng biến thiên, ta thấy trên khoảng (0; 12), hàm số V(h) đạt giá trị lớn nhất bằng 400π/9 tại h = 4.

Vậy h = 4 cm thì khối trụ có thể tích lớn nhất.