Bài 16 trang 66 Toán 12 tập 1 Chân trời sáng tạo

08:19:5421/03/2024

Tứ diện đều là một hình khối đặc biệt có nhiều tính chất đối xứng, được ứng dụng rộng rãi trong cả toán học và hóa học. Bài toán này sẽ giúp bạn hiểu rõ hơn về mối liên hệ giữa hình học và cấu trúc phân tử bằng cách chứng minh một tính chất nổi tiếng của phân tử metan (CH₄). Bài viết này sẽ hướng dẫn bạn giải chi tiết Bài 16 trang 66 Toán 12 tập 1 sách Chân trời sáng tạo, tập trung vào việc sử dụng các phép toán vectơ để chứng minh góc liên kết H-C-H.

Đề bài:

Cho biết bốn đoạn thẳng nối từ một đỉnh của tứ diện đến trọng tâm mặt đối diện luôn cắt nhau tại một điểm gọi là trọng tâm của tứ diện đó.

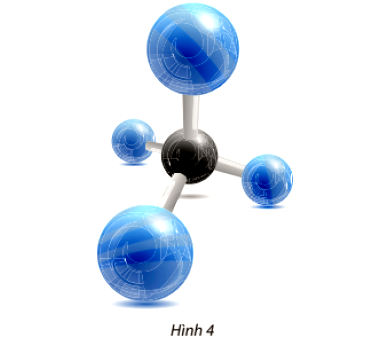
Một phân tử metan CH₄ được cấu tạo bởi bốn nguyên tử hydrogen ở các đỉnh của một tứ diện đều và một nguyên tử carbon ở trọng tâm của tứ diện.

Góc liên kết là góc tạo bởi liên kết H - C - H là góc giữa các đường nối nguyên tử carbon với hai trong số các nguyên tử hydrogen.

Chứng mimh rằng góc liên kết này gần bằng 109,5^o.

Bài 16 trang 66 Toán 12 tập 1 Chân trời sáng tạo

Phân tích và Hướng dẫn giải:

Để giải quyết bài toán này, chúng ta sẽ sử dụng phương pháp vectơ. Trọng tâm của tứ diện là điểm G thỏa mãn tính chất $\vec{GA}+\vec{GB}+\vec{GC}+\vec{GD}=\vec{0}$ . Góc liên kết H-C-H chính là góc tạo bởi hai vectơ nối từ nguyên tử carbon (đặt tại trọng tâm G) đến hai nguyên tử hydrogen bất kỳ (đặt tại các đỉnh A, B, C, D của tứ diện). Chẳng hạn, góc H-C-H có thể là góc giữa hai vectơ $\vec{GA}$ và $\vec{GB}$ .

Chúng ta sẽ sử dụng các tính chất sau của vectơ:

Tính chất trọng tâm tứ diện:

$\vec{GA}+\vec{GB}+\vec{GC}+\vec{GD}=\vec{0}$
Tích vô hướng:

$\vec{a}\cdot\vec{b}=|\vec{a}|\cdot|\vec{b}|\cdot\cos(\vec{a},\vec{b})$
Bình phương độ dài vectơ:

$|\vec{a}|^2=\vec{a}\cdot\vec{a}$

Từ các tính chất trên, chúng ta có thể thiết lập một phương trình để tìm giá trị của $\cos(\vec{a},\vec{b})$ .

Lời giải chi tiết:

Ta có hình minh họa:

Giải bài 16 trang 66 Toán 12 tập 1 Chân trời sáng tạo

Gọi tứ diện đều là ABCD và G là trọng tâm của tứ diện.

Đặt $\vec{a}=\vec{GA}$ , $\vec{b}=\vec{GB}$ , $\vec{c}=\vec{GC}$ , và $\vec{d}=\vec{GD}$ .

Vì G là trọng tâm của tứ diện ABCD, ta có:

$\vec{GA}+\vec{GB}+\vec{GC}+\vec{GD}=\vec{0}\Rightarrow\vec{a}+\vec{b}+\vec{c}+\vec{d}=\vec{0}$

Bình phương cả hai vế của đẳng thức này:

$(\vec{a}+\vec{b}+\vec{c}+\vec{d})^2=0$

$\vec{a}^2+\vec{b}^2+\vec{c}^2+\vec{d}^2+2(\vec{a}\cdot\vec{b}+\vec{a}\cdot\vec{c}+\vec{a}\cdot\vec{d}+\vec{b}\cdot\vec{c}+\vec{b}\cdot\vec{d}+\vec{c}\cdot\vec{d})=0$

Vì đây là tứ diện đều và G là trọng tâm, khoảng cách từ G đến các đỉnh là bằng nhau.

Tức là: $|\vec{a}|=|\vec{b}|=|\vec{c}|=|\vec{d}|$

Hơn nữa, góc giữa bất kỳ cặp vectơ nào trong số các vectơ này cũng bằng nhau, ví dụ:

$\cos(\vec{a},\vec{b})=\cos(\vec{a},\vec{c})=...=\cos\alpha$

Và tích vô hướng giữa bất kỳ cặp vectơ nào cũng bằng nhau:

$\vec{a}\cdot\vec{b}=\vec{a}\cdot\vec{c}=...$

Do đó, ta có thể rút gọn phương trình trên:

$4|\vec{a}|^2+2\cdot 6\cdot(\vec{a}\cdot\vec{b})=0$

$4|\vec{a}|^2+12(\vec{a}\cdot\vec{b})=0$

$4|\vec{a}|^2=-12(\vec{a}\cdot\vec{b})$

$|\vec{a}|^2=-3(\vec{a}\cdot\vec{b})$

Từ công thức tích vô hướng $\vec{a}\cdot\vec{b}=|\vec{a}|\cdot|\vec{b}|\cdot\cos\alpha$

và vì $|\vec{a}|=|\vec{b}|$ , ta có $\vec{a}\cdot\vec{b}=|\vec{a}|^2\cos\alpha$ .

Thay vào phương trình trên:

$|\vec{a}|^2=-3(|\vec{a}|^2\cos\alpha)$

Vì $|\vec{a}|\ne 0$ , ta có thể chia cả hai vế cho $|\vec{a}|^2$ :

$1=-3\cos\alpha\Rightarrow\cos\alpha=-\frac{1}{3}$

Vậy, góc liên kết $\alpha$ là:

$\alpha=\arccos\left(-\frac{1}{3}\right)\approx 109,47^\circ$

Làm tròn, ta được $\alpha\approx 109,5^\circ$ .

Bài toán này là một ví dụ tuyệt vời về việc áp dụng phương pháp vectơ để giải quyết các bài toán hình học phức tạp. Bằng cách sử dụng tính chất đặc trưng của trọng tâm tứ diện, chúng ta đã biến bài toán hình học không gian thành một bài toán đại số đơn giản.

Tư duy véc-tơ cho phép chúng ta biểu diễn các đối tượng hình học (điểm, đường, góc) dưới dạng các đại lượng toán học có thể tính toán được.
Tích vô hướng là công cụ chính để liên kết độ dài và góc giữa các véc-tơ.

Nắm vững cách sử dụng các tính chất này không chỉ giúp bạn giải quyết các bài toán trong sách giáo khoa mà còn mở ra một cách tiếp cận mới để hiểu về cấu trúc của các phân tử và các đối tượng ba chiều khác.

• Xem thêm:

Bài 10 trang 65 Toán 12 tập 1 Chân trời sáng tạo: Tìm tọa độ của điểm P được biểu diễn trong hình 2 và tính khoảng cách OP...

Bài 11 trang 66 Toán 12 tập 1 Chân trời sáng tạo: Cho $\overrightarrow{u}$ = (2; -5; 3), $\overrightarrow{v}$ = (0; 2; -1), $\overrightarrow{w}$ = (1; 7; 2). Tìm tạo độ của vectơ...