Bài 9 trang 65 Toán 12 tập 1 Chân trời sáng tạo

Đề bài:

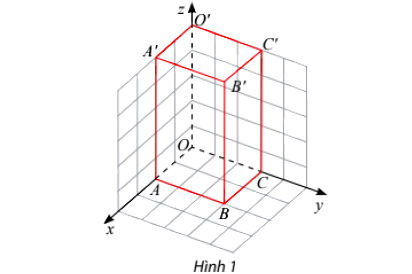
Trong không gian Oxyz, cho hình hộp chữ nhật OABC.O'A'B'C' như Hình 1, biết B'(2; 3; 5).

a) Tìm tọa đọ các đỉnh còn lại của hình hộp

b) Tính độ dài đường chéo OB' của hình hộp chữ nhật đó.

Phân tích và Hướng dẫn giải:

Bài toán này dựa trên việc hiểu rõ cấu trúc của hình hộp chữ nhật trong hệ tọa độ Oxyz.

a) Tọa độ các đỉnh: Điểm gốc O(0; 0; 0) là một đỉnh của hình hộp. Các đỉnh còn lại có tọa độ dễ dàng xác định dựa trên tọa độ của đỉnh B'(2; 3; 5) và tính chất của hình hộp chữ nhật.

• Hoành độ (x): Các đỉnh nằm trên mặt phẳng OAB'C' có hoành độ x = 0 hoặc x = 2.

• Tung độ (y): Các đỉnh nằm trên mặt phẳng O'A'B'C' có tung độ y = 0 hoặc y = 3.

• Cao độ (z): Các đỉnh nằm trên mặt phẳng OAB'C có cao độ z = 0 hoặc z = 5.

b) Độ dài đường chéo OB': Độ dài đường chéo OB' chính là khoảng cách từ gốc tọa độ O(0; 0; 0) đến điểm B'(2; 3; 5). Ta áp dụng công thức tính khoảng cách giữa hai điểm trong không gian Oxyz.

Công thức tính độ dài đoạn thẳng nối hai điểm M(x₁​;y₁​;z₁​) và N(x₂​;y₂​;z₂​) là: 

Lời giải chi tiết:

a) Tìm tọa độ các đỉnh còn lại

Dựa vào tọa độ của B'(2; 3; 5) và vị trí của các đỉnh so với hệ trục tọa độ, ta có:

• Đỉnh O: Vì O là gốc tọa độ, nên O(0; 0; 0)

• Đỉnh A: Nằm trên trục Ox, có cùng tung độ và cao độ với O, cùng hoành độ với B', nên A(2; 0; 0).

• Đỉnh C: Nằm trên trục Oy, có cùng hoành độ và cao độ với O, cùng tung độ với B', nên C(0; 3; 0).

• Đỉnh O': Nằm trên trục Oz, có cùng hoành độ và tung độ với O, cùng cao độ với B', nên O'(0; 0; 5).

• Đỉnh B: Nằm trên mặt phẳng Oxy, có cùng hoành độ với A và tung độ với C, nên B(2; 3; 0).

• Đỉnh A': Nằm trên mặt phẳng chứa điểm B', có cùng hoành độ với A và cùng cao độ với B', nên A'(2; 0; 5).

• Đỉnh C': Nằm trên mặt phẳng chứa điểm B', có cùng tung độ với C và cùng cao độ với B', nên C'(0; 3; 5).

Vậy, tọa độ các đỉnh là: O(0; 0; 0), A(2; 0; 0), B(2; 3; 0), C(0; 3; 0). O'(0; 0; 5), A'(2; 0; 5), B'(2; 3; 5), C'(0; 3; 5).

b) Tính độ dài đường chéo OB'

Áp dụng công thức tính khoảng cách giữa hai điểm O(0; 0; 0) và B'(2; 3; 5).

Độ dài đường chéo OB'là: