Giải bài 5 trang 32 SGK Toán 10 Chân trời sáng tạo Tập 1

Đề bài:

Miền không gạch chéo (không kể bờ d) trong mỗi hình dưới đây là miền nghiệm của bất phương trình nào?

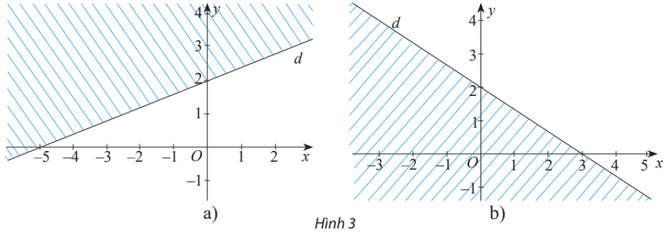
Phân tích và Hướng dẫn giải

Để giải quyết bài toán này, các em cần làm theo hai bước chính:

1. Xác định phương trình đường thẳng bờ: Dựa vào hai điểm mà đường thẳng $d$ đi qua, các em sẽ lập hệ phương trình để tìm ra phương trình đường thẳng $y=ax+b$ hoặc $Ax+By+C=0$.

2. Xác định dấu của bất phương trình:

   • Chọn một điểm thử: Lấy một điểm thuộc miền nghiệm (thường là gốc tọa độ $O(0;0)$ nếu nó nằm trong miền không gạch chéo) và thay tọa độ của nó vào vế trái của phương trình đường thẳng.

   • So sánh và kết luận: Dựa vào kết quả so sánh với 0, ta sẽ xác định được dấu của bất phương trình (> hoặc <).

   • Lưu ý: Đề bài cho biết miền nghiệm không kể bờ $d$, nên dấu bất phương trình sẽ là ">" hoặc "<".

Lời giải chi tiết:

a) Giả sử phương trình đường thẳng d có dạng là y = ax + b

Đường thẳng d đi qua hai điểm (0; 2) và (- 5; 0) nên ta có:

Giải hệ trên ta được a = 2/5, b = 2. Suy ra y = 2x/5 + 2 hay 2x – 5y + 10 = 0.

Vậy ta có phương trình đường thẳng d là 2x – 5y + 10 = 0.

Mặt khác O (0; 0) không thuộc d và thuộc miền nghiệm của bất phương trình.

Mà  2.0 – 5.0 + 10 = 10 > 0.

Hơn nữa miền nghiệm không kể đường thẳng d nên bất phương trình cần tìm là 2x – 5y + 10 > 0.

b) Giả sử phương trình đường thẳng d có dạng là y = ax + b

Đường thẳng d đi qua hai điểm (3; 0) và (0; 2) nên ta có:

Giải hệ trên ta được a =-2/3 , b = 2. Suy ra y = -2x/3 + 2 hay 2x + 3y – 6 = 0.

Vậy ta có phương trình đường thẳng d là 2x + 3y – 6 = 0.

Mặt khác O (0; 0) không thuộc d và  không thuộc miền nghiệm của bất phương trình.

Mà 2.0 + 3.0 – 6  = – 6  < 0.

Hơn nữa miền nghiệm của bất phương trình không kể đường thẳng d nên bất phương trình cần tìm là 2x + 3y – 6 > 0.