Giải bài 6 trang 78 Toán 10 Chân trời sáng tạo (SGK Tập 1)

Đề bài:

Một người đứng ở trên một tháp truyền hình cao 352 m so với mặt đất, muốn xác định khoảng cách giữa hai cột mốc trên mặt đất bên dưới.

Người đó quan sát thấy góc được tạo bởi hai đường ngắm tới hai mốc này là 43°, góc giữa phương thẳng đứng và đường ngắm tới một điểm mốc trên mặt đất là 62° và điểm mốc khác là 54° (Hình 11). Tính khoảng cách giữa hai cột mốc này.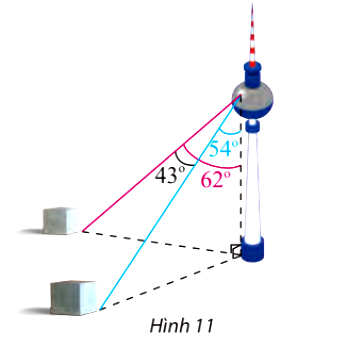 

Phân tích và Hướng dẫn giải:

Để giải bài toán này, chúng ta sẽ thực hiện các bước sau:

1. Mô hình hóa bài toán: Coi tháp truyền hình là đoạn AD, hai mốc là B và C. Ta có hai tam giác vuông ABD và ACD, và một tam giác ABC.

2. Sử dụng hệ thức lượng: Áp dụng hệ thức lượng trong các tam giác vuông ABD và ACD để tính độ dài các cạnh AB và AC (đường ngắm).

3. Sử dụng định lí côsin: Áp dụng định lí côsin cho tam giác ABC để tính độ dài cạnh BC khi biết hai cạnh AB, AC và góc xen giữa chúng.

Lời giải chi tiết:

Gọi vị trí người đứng ở trên tháp truyền hình là A, hai cột mốc ở dưới đất lần lượt là B và C, chân tháp truyền hình là D.

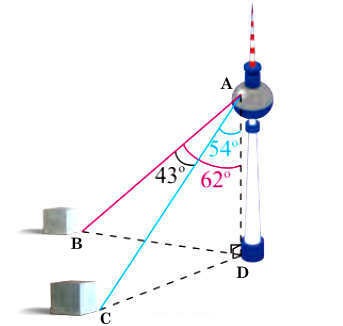
Khi đó ta có các tam giác ABD và ACD vuông tại D.

, ,  và AD = 352 m.

Trong tam giác ABD vuông tại D ta có:

Trong tam giác ACD vuông tại D ta có:

Áp dụng định lí côsin cho tam giác ABC ta có:

BC² = AB² + AC² – 2.AB.AC.

= 749,8² + 598,9² – 2.749,8.598,9. cos43° ≈ 264 044,9

Vậy khoảng cách giữa hai cột mốc khoảng 513,9 m.