Hotline 0962 782 149

Giải bài 9 trang 73 Toán 10 Chân trời sáng tạo (SGK Tập 1)

15:52:2111/11/2022

Cho tam giác ABC có góc B nhọn, AD và CE là hai đường cao...

Bài 9 trang 73 Toán 10 Chân trời sáng tạo (SGK Tập 1): Cho tam giác ABC có góc B nhọn, AD và CE là hai đường cao.

a) Chứng minh: $\dpi{100} \small \frac{S_{BDE}}{S_{BAC}}=\frac{BD.BE}{BA.BC}$

b) Biết rằng S_ABC = 9S_BDE và DE = 2√2. Tính cosB và bán kính đường tròn ngoại tiếp tam giác ABC.

Giải bài 9 trang 73 Toán 10 Chân trời sáng tạo (SGK Tập 1):

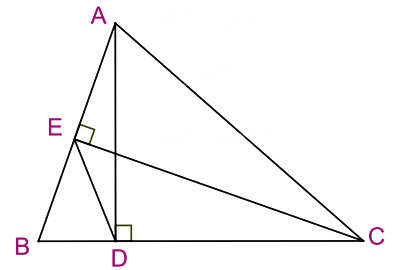
Giải bài 9 trang 73 SGK Toán 10 Chân trời sáng tạo

a) Chứng minh: $\dpi{100} \small \frac{S_{BDE}}{S_{BAC}}=\frac{BD.BE}{BA.BC}$

Áp dụng công thức: $\small S=\frac{1}{2}ac.sinB$

Cho tam giác ABC và BED, ta có:

$\small S_{ABC}=\frac{1}{2}BA.BC.sinB$

$\small S_{BED}=\frac{1}{2}BE.BD.sinB$

Nên: $\small \frac{S_{BCE}}{S_{BAC}}=\frac{\frac{1}{2}BE.BE.sinB}{\frac{1}{2}BA.BC.sinB}=\frac{BE.BD}{BA.BC}$

b) Tính cosB và bán kính đường tròn ngoại tiếp tam giác ABC.

Ta có: $\small cosB=\frac{BD}{BA}=\frac{BE}{BC}$

Mà: $\small \frac{S_{BDE}}{S_{BAC}}=\frac{1}{9}\Rightarrow \frac{BD.BE}{BA.BC}=\frac{1}{9}$

$\small \Rightarrow cosB=\frac{BD}{BA}=\frac{BE}{BC}=\frac{1}{3}$

+) Xét tam giác ABC và tam giác DEB ta có:

$\small \frac{BE}{BC}=\frac{BD}{BA}=\frac{1}{3}$ và góc B chung.

Suy ra: ΔABC ∼ ΔDEB (c-g-c)

$\small \Rightarrow \frac{DE}{AC}=\frac{1}{3}\Rightarrow AC=3DE=3.2\sqrt{2}=6\sqrt{2}$

Ta có:

$\small cosB=\frac{1}{3}\Rightarrow sinB=\sqrt{1-\left ( \frac{1}{3} \right )^2}=\frac{2\sqrt{2}}{3}$ (do B là góc nhọn nên sinB>0)

+ Áp dụng định lí sin trong tam giác ABC ta có:

$\small \frac{AC}{sinB}=2R\Rightarrow R=\frac{AC}{2.sinB}=\frac{6\sqrt{2}}{2.\frac{2\sqrt{2}}{3}}=\frac{9}{2}$

Vậy bán đường tròn ngoại tiếp tam giác ABC là: 9/2 (đơn vị độ dài)

Hy vọng với lời giải bài 9 trang 73 Toán 10 Chân trời Sáng tạo (SGK Tập 1) ở trên đã giúp các em hiểu và nắm vững phần kiến thức này. Mọi góp ý và thắc mắc các em hãy để lại nhận xét dưới bài viết để Hay Học Hỏi ghi nhận và hỗ trợ, chúc các em học tốt.

• Xem giải bài tập Toán 10 Chân trời sáng tạo SGK tập 1 cùng chuyên mục

> Bài 1 trang 72 Toán 10 Chân trời sáng tạo (SGK Tập 1): Tính độ dài cạnh x trong các tam giác sau:...

> Bài 2 trang 72 Toán 10 Chân trời sáng tạo (SGK Tập 1): Tính độ dài cạnh c trong tam giác ABC ở Hình 14...

> Bài 3 trang 72 Toán 10 Chân trời sáng tạo (SGK Tập 1): Cho tam giác ABC, biết cạnh a = 152, $\small \widehat{B}=79^0,\: \widehat{C}=61^0$ . Tính các góc, các cạnh...