Giải bài 6 trang 56 Toán 10 Chân trời sáng tạo (SGK Tập 1)

Đề bài:

Vẽ đồ thị các hàm số sau:

a) y = 2x² + 4x – 1;

b) y = -x² + 2x + 3;

c) y = -3x² + 6x;

d) y = 2x² – 5.

Phân tích và Hướng dẫn giải:

Để vẽ đồ thị của hàm số bậc hai y=ax²+bx+c, chúng ta cần xác định các yếu tố sau:

1. Tọa độ đỉnh: Đỉnh của parabol có hoành độ .

2. Trục đối xứng: Đường thẳng x=x_S​.

3. Chiều quay của bề lõm:

   • Nếu $a>0$, parabol quay lên.

   • Nếu $a<0$, parabol quay xuống.

4. Giao điểm với các trục tọa độ:

   • Giao với trục tung (cho $x=0$).

   • Giao với trục hoành (cho $y=0$).

5. Lập bảng giá trị: Lấy thêm một vài điểm để đồ thị chính xác hơn.

Lời giải chi tiết:

a) y = 2x² + 4x – 1

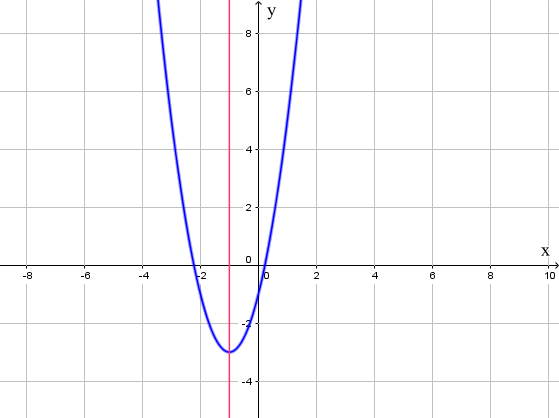
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = 2x² + 4x – 1 là một parabol (P):

- Có đỉnh S với hoành độ x_S = -1, tung độ y_S = -3;

- Có trục đối xứng là đường thẳng x = -1 (đường thẳng này đi qua đỉnh S và song song với trục Oy);

- Bề lõm quay lên trên vì a > 0;

- Cắt trục tung tại điểm có tung độ bằng -1, tức là đồ thị đi qua điểm có tọa độ (0; -1).

Ngoài ra, phương trình 2x² + 4x – 1 = 0 có hai nghiệm phân biệt:

Nên đồ thị hàm số cắt trục hoành tại hai điểm có tọa độ:

Ta được đồ thị hàm số như sau:

b) y = -x² + 2x + 3

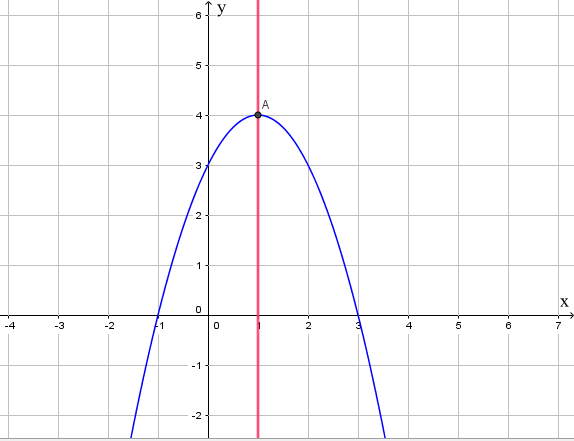
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = -x² + 2x + 3 là một parabol (P):

- Có đỉnh S với hoành độ x_S = 1, tung độ y_S = 4;

- Có trục đối xứng là đường thẳng x = 1 (đường thẳng này đi qua đỉnh S và song song với trục Oy);

- Bề lõm quay xuống dưới vì a < 0;

- Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).

Ngoài ra, phương trình -x² + 2x + 3 = 0 có hai nghiệm phân biệt x₁ = 3 và x₂ = -1 nên đồ thị hàm số cắt trục hoành tại hai điểm có tọa độ (3; 0) và (-1; 0).

Ta được đồ thị hàm số như sau:

c) y = -3x² + 6x

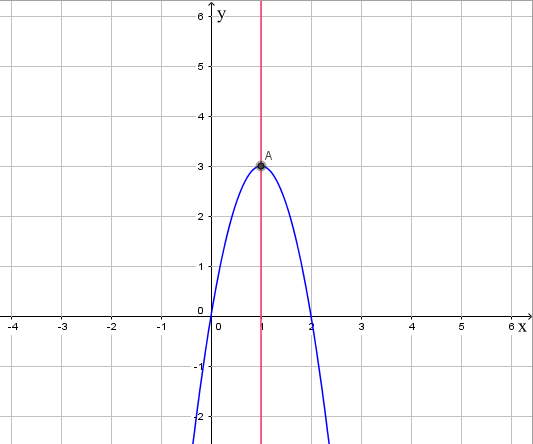
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = -3x² + 6x là một parabol (P):

- Có đỉnh S với hoành độ x_S = 1, tung độ y_S = 3;

- Có trục đối xứng là đường thẳng x = 1 (đường thẳng này đi qua đỉnh S và song song với trục Oy);

- Bề lõm quay xuống dưới vì a < 0;

- Cắt trục tung tại điểm có tung độ bằng 0, tức là đồ thị đi qua điểm có tọa độ (0; 0).

Ngoài ra, phương trình -3x² + 6x = 0 có hai nghiệm phân biệt x₁ = 0 và x₂ = 2 nên đồ thị hàm số cắt trục hoành tại hai điểm có tọa độ (0; 0) và (2; 0).

Ta được đồ thị hàm số như sau:

d) y = 2x² – 5

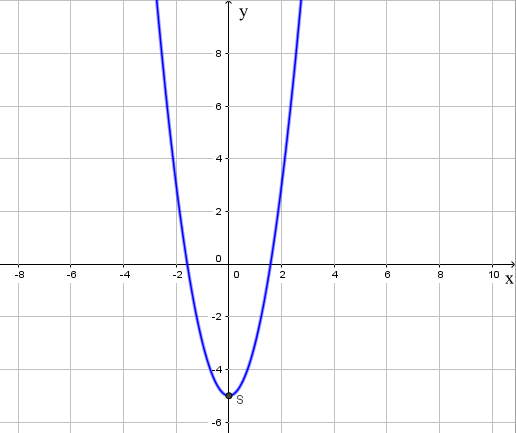
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = 2x² – 5 là một parabol (P):

- Có đỉnh S với hoành độ x_S = 0, tung độ y_S = -5;

- Có trục đối xứng là đường thẳng x = 0 (đường thẳng này đi qua đỉnh S và song song với trục Oy);

- Bề lõm quay lên trên vì a > 0;

- Cắt trục tung tại điểm có tung độ bằng -5, tức là đồ thị đi qua điểm có tọa độ (0; -5).

Ngoài ra, phương trình 2x² – 5 = 0 có hai nghiệm phân biệt

Nên đồ thị hàm số cắt trục hoành tại hai điểm có tọa độ:

Ta được đồ thị hàm số như sau: