Giải bài 5 trang 65 Toán 10 Chân trời sáng tạo (SGK Tập 1)

Đề bài:

Chứng minh rằng với mọi góc α (0° ≤ α  ≤ 180°), ta đều có:

a) cos²α  + sin²α  = 1;

b) tanα.cotα  = 1 (0° < α < 180°, α ≠ 90°).

c) 1 + tan²α  = 1/cos²α  (α ≠ 90°);

d) 1 + cot² α  =  1/sin²α  (0° < α < 180°).

Phân tích và Hướng dẫn giải:

Để chứng minh các đẳng thức lượng giác, chúng ta sẽ sử dụng các định nghĩa và công thức cơ bản:

1. Định nghĩa: sinα=MH/OM​, cosα=OH/OM​, tanα=MH​/OH, cotα=OH​/MH.

2. Định lí Pythagoras: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

3. Công thức liên hệ: tanα=sinα/cosα​ và cotα=cosα/sinα​.

Chúng ta sẽ sử dụng các kiến thức này để biến đổi một vế của đẳng thức về vế còn lại.

Lời giải chi tiết:

a) cos²α  + sin²α  = 1

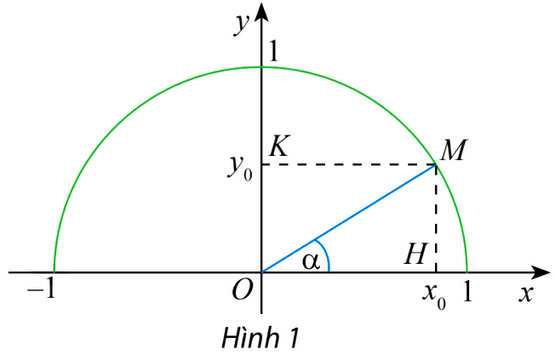
Trên nửa đường tròn đơn vị, lấy điểm M sao cho

Gọi H, K lần lượt là các hình chiếu vuông góc của M trên Ox, Oy.

Ta có tam giác vuông OHM vuông tại H và 

Do đó: 

Suy ra:  cos²α  + sin²α  = OH² + MH² = OM² = 1

Vậy cos²α  + sin²α  = 1.

b) tanα.cotα  = 1 (0° < α < 180°, α ≠ 90°).

Ta có: tanα = sinα/cosα; cotα = cosα/sinα

Suy ra:  

c) 1 + tan²α  = 1/cos²α  (α ≠ 90°)

Với α ≠ 90° ta có: 

Suy ra:

d) 1 + cot² α  =  1/sin²α  (0° < α < 180°)

Ta có: 

Suy ra: