Giải bài 4 trang 78 Toán 10 Chân trời sáng tạo (SGK Tập 1)

Đề bài:

Tính chiều cao AB của một ngọn núi. Biết tại hai điểm C, D cách nhau 1 km trên mặt đất (B, C, D thẳng hàng), người ta nhìn thấy đỉnh A của núi với góc nâng lần lượt là 32° và 40° (Hình 9).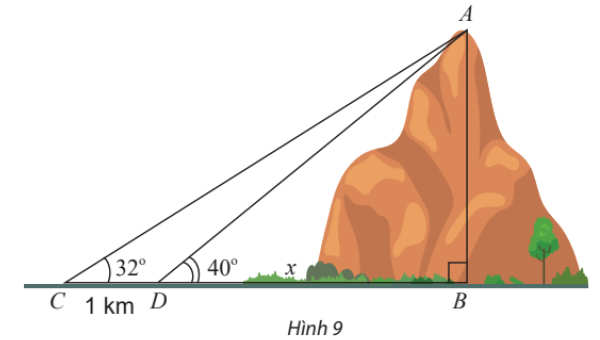

Phân tích và Hướng dẫn giải

Để tính chiều cao AB của ngọn núi, chúng ta sẽ dựa vào các thông tin đã cho và sử dụng hệ thức lượng trong tam giác vuông.

1. Xác định các tam giác vuông: Bài toán có hai tam giác vuông chính là $△ABC$ và $△ABD$, đều vuông tại B.

2. Đặt ẩn: Gọi độ dài cạnh BD là $x$. Từ đó, ta có thể biểu diễn các cạnh khác theo $x$.

3. Lập hệ phương trình: Sử dụng hệ thức lượng (cụ thể là hàm tan) cho cả hai tam giác vuông để biểu diễn chiều cao AB theo $x$ và các góc đã biết.

4. Giải phương trình: Từ hai biểu thức của AB, chúng ta sẽ lập một phương trình để tìm giá trị của $x$. Sau khi có $x$, ta dễ dàng tính được chiều cao AB.

Lời giải chi tiết:

Đặt BD = x km, khi đó ta có CB = BD + CD = x + 1.

Trong tam giác ABC vuông tại B ta có:

 (1)

Trong tam giác ABD vuông tại B ta lại có:

  (2)

Từ (1) và (2) ta có:

Suy ra AB = x.tan40° ≈ 2,92.tan40° ≈ 2,45 km.

Vậy chiều cao AB của một ngọn núi khoảng 2,45 km.