Giải bài 3 trang 32 SGK Toán 10 Chân trời sáng tạo Tập 1

Đề bài:

Biểu diễn miền nghiệm của các bất phương trình sau trên mặt phẳng tọa độ oxy

a) – x + 2 + 2(y – 2) < 2(1 – x)

b) 3(x – 1 ) + 4(y – 2) < 5x – 3.

Phân tích và Hướng dẫn giải

Để biểu diễn miền nghiệm của một bất phương trình phức tạp, các em cần thực hiện các bước sau:

1. Biến đổi bất phương trình: Chuyển tất cả các số hạng về một vế và rút gọn để đưa bất phương trình về dạng chuẩn $ax+by+c>0$ (hoặc $<$, $\ge$, $\le$).

2. Vẽ đường thẳng bờ: Vẽ đường thẳng tương ứng với bất phương trình đã rút gọn (thay dấu bất đẳng thức bằng dấu bằng).

3. Chọn điểm thử: Chọn một điểm bất kỳ không nằm trên đường thẳng đó (gốc tọa độ $O(0;0)$ là lựa chọn tốt nhất nếu đường thẳng không đi qua nó).

4. Xác định miền nghiệm: Dựa vào kết quả kiểm tra ở bước 3 để xác định nửa mặt phẳng chứa miền nghiệm.

Lời giải chi tiết:

a) Ta có: – x + 2 + 2(y – 2 ) < 2(1 – x)

⇔ – x + 2 + 2(y – 2 ) – 2(1 – x) < 0

⇔ – x + 2 + 2y – 4  – 2 + 2x < 0

⇔ x + 2y – 4 < 0

Ta sẽ biểu diễn miền nghiệm của bất phương trình x + 2y – 4 < 0.

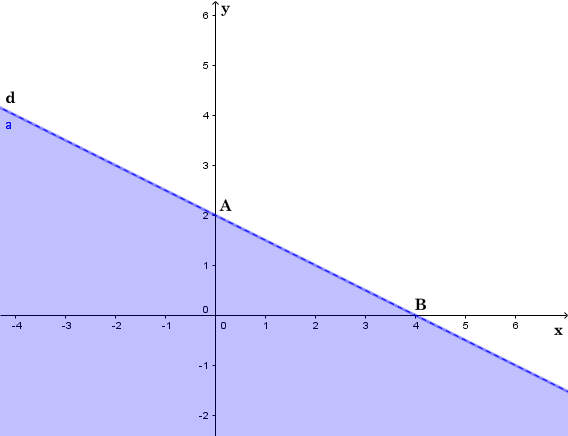
Vẽ đường thẳng d: x + 2y – 4 = 0 đi qua điểm A(0; 2) và B (4 ; 0).

Xét gốc tọa độ O(0 ; 0). Ta thấy O ∉ d và  0 + 2.0 – 4 = – 4 < 0.

Suy ra (0 ; 0) là nghiệm của bất phương trình x + 2y – 4 < 0.

Do đó, miền nghiệm của bất phương trình x + 2y – 4 < 0 là nửa mặt phẳng không kể bờ d, chứa điểm O (là miền tô màu trong hình sau).

b) Ta có: 3(x – 1 ) + 4(y – 2) < 5x – 3

⇔ 3x – 3  + 4y – 8 – 5x + 3 < 0

⇔ –  2x + 4y – 8 < 0

⇔ – x + 2y – 4 < 0

Ta sẽ biểu diễn miền nghiệm của bất phương trình – x + 2y – 4 < 0

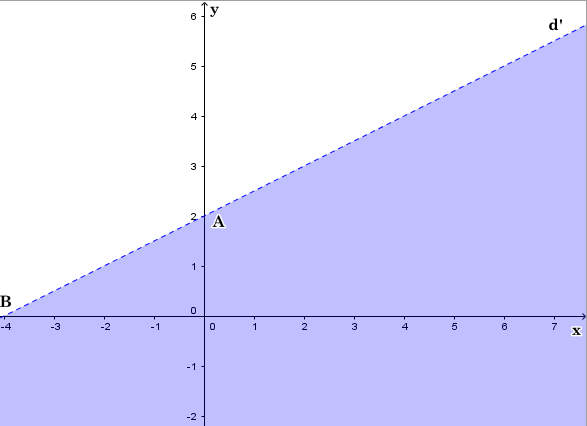
Vẽ đường thẳng d' : – x + 2y – 4 = 0 đi qua điểm A(0; 2) và B (– 4 ; 0).

Xét gốc tọa độ O(0 ; 0). Ta thấy O ∉ d' và  – 0 + 2. 0 – 4 = – 4 < 0.

Suy ra (0 ; 0) là nghiệm của bất phương trình  – x + 2y – 4 < 0.

Do đó, miền nghiệm của bất phương trình –x + 2y – 4 < 0 là nửa mặt phẳng không kể bờ d', chứa điểm O (là miền tô màu trong hình sau).