Giải bài 4 trang 25 Toán 10 tập 1 SGK Chân trời sáng tạo

Đề bài:

Cho A và B là hai tập hợp bất kì. Trong mỗi cặp tập hợp sau đây, tập hợp nào là tập con của tập hợp còn lại? Hãy giải thích bằng cách sử dụng biểu đồ Ven.

a) A và A∪B;

b) A và A∩B.

Phân tích và Hướng dẫn giải:

Để giải bài toán này, các bạn cần hiểu rõ định nghĩa về tập hợp con và cách biểu diễn các phép toán trên biểu đồ Venn.

• Tập hợp con: Tập hợp $A$ được gọi là tập hợp con của tập hợp $B$ (kí hiệu $A\subset B$) nếu mọi phần tử của $A$ đều là phần tử của $B$.

• Biểu đồ Venn: Là một sơ đồ sử dụng các hình tròn lồng vào nhau để thể hiện mối quan hệ giữa các tập hợp.

  • Vùng chung giữa hai hình tròn biểu thị tập hợp giao ($A\cap B$).

  • Toàn bộ các vùng của hai hình tròn biểu thị tập hợp hợp ($A\cup B$).

Dựa vào biểu đồ Venn, ta sẽ dễ dàng quan sát được một tập hợp có nằm hoàn toàn bên trong một tập hợp khác hay không.

Lời giải chi tiết:

Ta có sơ đồ Ven như sau:

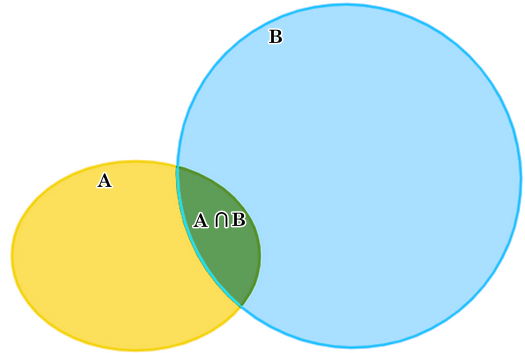
a) A và A∪B;

+ Ta thấy tập hợp A ∪ B bao gồm phần màu vàng, phần màu xanh lá cây và phần màu xanh da trời.

+ Tập hợp A chứa phần màu cam cộng màu xanh lá cây nằm hoàn toàn trong tập hợp A ∪ B.

Do đó tập A là tập con của tập A ∪ B.

Ta viết A ⊂ (A∪B).

b) A và A∩B.

Tập hợp A ∩ B là phần màu xanh lá cây và nằm hoàn toàn trong tập hợp A.

Nên tập A ∩ B  là tập con của tập A.

Ta viết (A ∩ B) ⊂ A.