Giải bài 6 trang 25 Toán 10 tập 1 SGK Chân trời sáng tạo

Đề bài:

Xác định các tập hợp sau đây:

a) (-∞; 0] U [-π; π]

b) [-3,5; 2] ∩ (-2; 3,5);

c) (-∞; √2] ∩ [1; +∞)

d) (-∞; √2] \ [1; +∞)

Phân tích và Hướng dẫn giải:

Để thực hiện các phép toán trên các tập hợp số, bạn có thể sử dụng phương pháp biểu diễn các tập hợp đó trên một trục số. Các bước thực hiện như sau:

1. Vẽ trục số: Vẽ một trục số, đánh dấu các điểm đầu mút của các khoảng trên đó.

2. Biểu diễn các tập hợp:

   • Với các phép toán hợp ($\cup$) hoặc hiệu ($\setminus$), bạn tô đậm các khoảng thuộc tập hợp.

   • Với phép toán giao ($\cap$), bạn gạch chéo các phần không thuộc tập hợp.

3. Xác định kết quả:

   • Phép hợp: Kết quả là toàn bộ các khoảng đã tô đậm.

   • Phép giao: Kết quả là phần không bị gạch chéo.

   • Phép hiệu: Kết quả là phần thuộc tập hợp bị trừ nhưng không thuộc tập hợp trừ.

Trong bài toán này, các số $\pi$ và ​ có thể được làm tròn để dễ dàng biểu diễn trên trục số.

Lời giải chi tiết:

a) Để xác định tập hợp A = (-∞; 0] U [-π; π], ta vẽ sơ đồ sau đây:

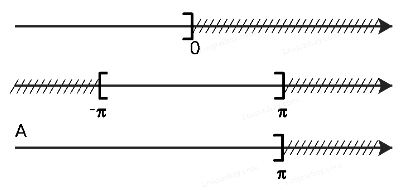
Từ sơ đồ, ta thấy A = (-∞; π]

b) Để xác định tập hợp B = [-3,5; 2] ∩ (-2; 3,5), ta vẽ sơ đồ sau đây:

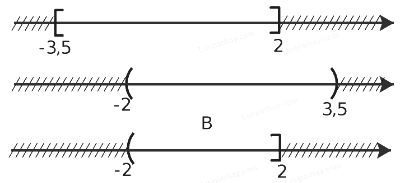Từ sơ đồ ta thấy B = (-2; 2]

c) Để xác định tập hợp C = (-∞; √2] ∩ [1; +∞), ta vẽ sơ đồ sau đây:

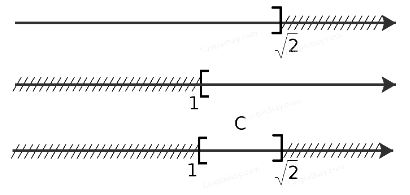Từ sơ đồ ta thấy C = [1; √2]

d) Để xác định tập hợp D = (-∞; √2] \ [1; +∞), ta vẽ sơ đồ sau đây:

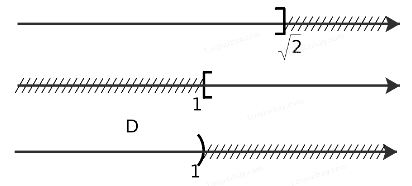Từ sơ đồ ta thấy D = (-∞; 1)