Bài 1 trang 70 Toán 8 Tập 2 Chân trời sáng tạo

Bài 1 trang 70 Toán 8 Tập 2 Chân trời sáng tạo: 

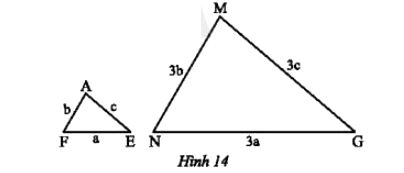
a) Tam giác AFE và MNG ở Hình 14 có đồng dạng với nhau không? Vì sao?

b) Biết tam giác AFE có chu vi bằng 15 cm. Tính chu vi tam giác MNG.

Phân Tích Hướng Dẫn Giải:

1. Đồng dạng (a): Hai tam giác $AFE$ và $MNG$ đồng dạng theo trường hợp c.c.c nếu tỉ số độ dài các cặp cạnh tương ứng là bằng nhau ($\frac{AF}{MN} = \frac{FE}{NG} = \frac{AE}{MG}$).

2. Tỉ số Chu vi (b): Tỉ số chu vi của hai tam giác đồng dạng bằng tỉ số đồng dạng $k$. Nếu $\triangle AFE \sim \triangle MNG$ với tỉ số $k$, thì $\frac{\text{Chu vi } AFE}{\text{Chu vi } MNG} = k$.

Giải bài 1 trang 70 Toán 8 Tập 2 Chân trời sáng tạo: 

a) Xét ∆AFE và ∆MNG có:

$\frac{AF}{MN}=\frac{b}{3b}=\frac{1}{3}$

$\frac{FE}{NG}=\frac{a}{3a}=\frac{1}{3}$

$\frac{AE}{MG}=\frac{c}{3c}=\frac{1}{3}$

Nên $\frac{AF}{MN}=\frac{FE}{NG}=\frac{AE}{MG}$

Vậy ΔAFE ᔕ ΔMNG (c.c.c).

b) Tam giác AFE đồng dạng với tam giác MNG theo tỉ số 1/3 nên tỉ số chu vi của hai tam giác đó cũng bằng 1/3.

Vậy chu vi ΔMNG là: 15.3 = 45 (cm).