Bài 7 trang 76 Toán 8 Tập 2 Chân trời sáng tạo

Bài 7 trang 76 Toán 8 Tập 2 Chân trời sáng tạo: 

Cho tam giác ABC vuông tại A có đường cao AH. Kẻ HM vuông góc với AB tại M.

a) Chứng minh rằng ΔAMH ᔕ ΔAHB.

b) Kẻ HN vuông góc với AC tại N. Chứng minh rằng AM.AB = AN.AC.

c) Chứng minh rằng ΔANM ᔕ ΔABC.

d) Cho biết AB = 9 cm, AC = 12 cm. Tính diện tích tam giác AMH.

Phân Tích và Hướng Dẫn Giải:

1. Chứng minh (a): Sử dụng trường hợp góc - góc (g.g) cho hai tam giác vuông có $\widehat{A}$ chung.

2. Chứng minh (b): Áp dụng hệ thức lượng $AH^2 = AM \cdot AB$ và $AH^2 = AN \cdot AC$ (cạnh góc vuông là trung bình nhân của cạnh huyền và hình chiếu).

3. Chứng minh (c): Sử dụng kết quả câu (b) để thiết lập tỉ số cạnh $\frac{AN}{AB} = \frac{AM}{AC}$ và áp dụng trường hợp cạnh - góc - cạnh (c.g.c) (với $\widehat{A}$ chung).

4. Tính $S_{AMN}$ (d):

   • Tính $BC$ (Pythagoras).

   • Tính $AH$ (Hệ thức lượng $AB \cdot AC = AH \cdot BC$).

   • Tính $AM, AN$ (dùng hệ thức lượng ở câu b).

   • $S_{AMN} = \frac{1}{2} AM \cdot AN$ (vì $\triangle AMN$ vuông tại $A$).

Giải bài 7 trang 76 Toán 8 Tập 2 Chân trời sáng tạo: 

Ta có hình minh hoạ như sau:

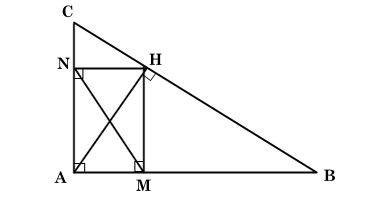
a) Xét hai tam giác vuông AMH và AHB có: $\widehat{A}$ chung

⇒ ΔAMH ᔕ ΔAHB (g.g)

b) ΔAMH ᔕ ΔAHB nên $\frac{AM}{AH}=\frac{AH}{AB}$

⇔ AM.AB = AH² (1)

Xét hai tam giác vuông ANH và AHC có:  $\widehat{A}$ chung

⇒ ΔANH ᔕ ΔAHC (g.g) nên

$\frac{AN}{AH}=\frac{AH}{AC}$ hay AN.AC = AH² (2)

Từ (1) và (2) ⇒ AM.AB = AN.AC (đpcm).

c) Ta có AM.AB = AN.AC,

Do đó  $\frac{AN}{AB}=\frac{AM}{AC}$

Xét hai tam giác vuông AMN và ABC có:

$\frac{AN}{AB}=\frac{AM}{AC}$ (chứng minh trên)

⇒ ΔANM ᔕ ΔABC (c.g.c)

d) Áp dụng định lí Pythagore vào tam giác ABC, ta có: 

BC² = AB² + AC² = 9² + 12² = 225.

Suy ra BC = 15 cm.

Xét hai tam giác vuông ABC và HBA có  chung

⇒ ΔABC ᔕ ΔHBA (g.g).

Suy ra $\frac{AC}{AH}=\frac{BC}{AB}$ (các cặp cạnh tương ứng).

Khi đó AH.BC = AB.AC hay AH.15 = 9.12.

⇒ AH = 7,2 cm.

• Từ (1): AM.AB = AH² nên

$AM=\frac{AH^2}{AB}$ $=\frac{7,2^2}{9}=5,76\: (cm)$

• Từ (2): AN.AC = AH² nên

$AN=\frac{AH^2}{AC}$ $=\frac{7,2^2}{12}=4,32\: (cm)$

Diện tích tam giác AMN là: 

$\frac{1}{2}.5,76.4,32=12,4416\: (cm^2)$

Vậy diện tích tam giác AMN là 12,4416 cm².