Bài 4 trang 76 Toán 8 Tập 2 Chân trời sáng tạo

Bài 4 trang 76 Toán 8 Tập 2 Chân trời sáng tạo: 

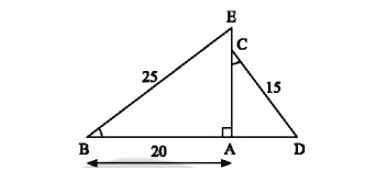
Trong Hình 11, cho biết  $\widehat{B}=\widehat{C}$, BE = 25 cm, AB = 20 cm, DC = 15 cm. Tính độ dài đoạn thẳng CE.

Phân Tích và Hướng Dẫn Giải:

1. Tính Độ dài trung gian ($AC$): Chứng minh $\triangle ABE \sim \triangle ACD$ (g.g) để thiết lập tỉ số đồng dạng và tính $AC$. (Lưu ý: Lời giải gốc có vẻ đã xem $A, C, E$ thẳng hàng).

2. Tính $AE$: Áp dụng Định lý Pythagoras cho $\triangle ABE$ vuông tại $A$.

3. Tính $CE$: Tính hiệu $CE = AE - AC$.

Giải bài 4 trang 76 Toán 8 Tập 2 Chân trời sáng tạo: 

Xét tam giác vuông ABE và ACD có $\widehat{B}=\widehat{C}$

Suy ra ΔABE ᔕ ΔACD (g.g)

Nên $\frac{AB}{AC}=\frac{BE}{CD}$ (các cạnh tương ứng).

hay $\frac{20}{AC}=\frac{25}{15}$ $\Rightarrow AC=\frac{20.15}{25}=12\: (cm) $

Vậy AC = 12 cm.

Áp dụng định lí Pythagore vào tam giác vuông ABE, ta có: 

BE² = AB² + AE²

Suy ra $AE=\sqrt{BE^2-AB^2}$ $=\sqrt{25^2-20^2}=\sqrt{225}=15$

Vì vậy, CE = AE – AC = 15 – 12 = 3 (cm).

Vậy CE = 3 cm.