Bài 6 trang 76 Toán 8 Tập 2 Chân trời sáng tạo

Bài 6 trang 76 Toán 8 Tập 2 Chân trời sáng tạo: 

Một người đo chiều cao của một tòa nhà nhờ một cọc chôn xuống đất, cọc cao 3 m và đặt cách xa tòa nhà 27 m. Sau khi người ấy lùi ra xa cách cọc 1,2 m thì nhìn thấy đầu cọc và đỉnh tòa nhà cùng nằm trên một đường thẳng. Hỏi tòa nhà cao bao nhiêu mét, biết rằng khoảng cách từ chân đến mắt người ấy là 1,5 m.

Phân Tích và Hướng Dẫn Giải:

1. Mô hình hóa: Đặt $C'$ là đỉnh tòa nhà, $A'$ là chân tòa nhà. $C$ là đỉnh cọc, $A$ là chân cọc. $E$ là mắt người đo, $D$ là chân người đo.

   • Chiều cao tòa nhà: $A'C' = h$ (cần tìm).

   • Chiều cao cọc: $AC = 3 \text{ m}$.

   • Khoảng cách $A'A = 27 \text{ m}$.

   • Chiều cao mắt: $DE = 1,5 \text{ m}$.

   • Khoảng cách $AD = 1,2 \text{ m}$.

2. Nguyên tắc Đồng dạng:

   • Gọi $B$ là giao điểm của đường thẳng nối mắt người ($E$), đầu cọc ($C$), và đỉnh tòa nhà ($C'$).

   • Ta có $\mathbf{\triangle DAB \sim \triangle EDB}$ (giả sử $C$ là giao điểm). Ta sẽ sử dụng các đường thẳng vuông góc để tạo tam giác đồng dạng.

3. Tạo Tam giác đồng dạng: Ta dựng các đường thẳng vuông góc với mặt đất để có: $\mathbf{A'C' // AC // DE}$.

   • Cặp 1: $\triangle EDB$ và $\triangle CAB$ (sai thứ tự). $\triangle EDB$ và $\triangle ECA$ (sai)

   • Cặp 1: $\triangle EDB$ và $\triangle CAB$ ($\triangle EDB$ và $\triangle ACB$). Giả sử $B$ là giao điểm của $EC'$ và $A'A$.

   • Cặp 2: $\triangle ACB$ và $\triangle A'C'B$.

Giải bài 6 trang 76 Toán 8 Tập 2 Chân trời sáng tạo: 

Ta có hình minh hoạ như sau:

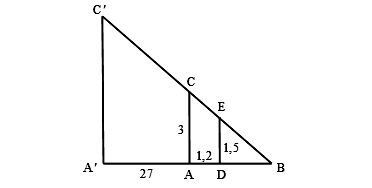
Gọi chiều cao của tòa nhà là h = A'C' và cọc tiêu AC = 3 m.

Khoảng cách từ chân đến mắt người đo là DE = 1,5 m.

Cọc xa cây một khoảng A'A = 27 m, và người cách cọc một khoảng AD = 1,2 m và gọi B là giao điểm của C'E và A'A.

Vì A'C' ⊥ A'B, AC ⊥ A'B, DE ⊥ A'B nên A'C' // AC // DE.

• ΔDEB ᔕ ΔACB (vì DE // AC)

Suy ra $\frac{DE}{AC}=\frac{DB}{AB}$ (các cặp cạnh tương ứng).

Mà AC = 3 m; DE = 1,5 m nên 

$\frac{1,5}{3}=\frac{DB}{AB}$ $\Rightarrow \frac{DB}{AB}$ $=\frac{1}{2}\Rightarrow \frac{DB}{1}=\frac{AB}{2}$

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

$\frac{DB}{1}=\frac{AB}{2}$ $=\frac{AB-DB}{2-1}$ $=\frac{AD}{1}=1,2$

⇒ DB = 1,2 và AB = 2.1,2 = 2,4

Vì vậy, A'B = A'A + AD + DB = 27 + 1,2 + 1,2 = 29,4 (m)

• ΔACB ᔕ ΔA'C'B (vì AC // A'C')

Suy ra $\frac{AB}{A'B}=\frac{AC}{A'C'}$ (các cặp cạnh tương ứng).

$\Rightarrow A'C'=\frac{AC.A'B}{AB}$ $=\frac{3.29,4}{2,4}=36,75\: (cm)$

Vậy tòa nhà cao 36,75 m.