Bài 16 trang 86 Toán 8 Tập 2 Chân trời sáng tạo

Bài 16 trang 86 Toán 8 Tập 2 Chân trời sáng tạo: 

Cho tam giác ABC vuông tại A (AB < AC). Kẻ đường cao AH (H ∈ BC).

a) Chứng minh rằng ΔABH ᔕ ΔCBA, suy ra AB² = BH.BC.

b) Vẽ HE vuông góc với AB tại E, vẽ HF vuông góc với AC tại F. Chứng minh rằng AE.AB = AF.AC.

c) Chứng minh rằng ΔAFE ᔕ ΔABC.

d) Qua A vẽ đường thẳng song song với BC cắt đường thẳng HF tại I. Vẽ IN vuông góc BC tại N. Chứng minh rằng ΔHNF ᔕ ΔHIC.

Giải bài 16 trang 86 Toán 8 Tập 2 Chân trời sáng tạo: 

Ta có hình minh họa như sau:

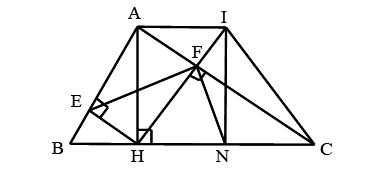
a) Xét tam giác vuông ABH và CBA ta có:

chung

Suy ra ΔABH ᔕ ΔCBA nên  

⇒ AB² = BH.BC

b) Tứ giác AEHF có 4 góc vuông

⇒ AEHF là hình chữ nhật 

Nên 

ΔABH ᔕ ΔCBA nên 

Xét tam giác AEF và ACB ta có:

chung

⇒ ΔAEF ᔕ ΔACB (g.g)

c) Theo câu b) ta có: ΔAEF ᔕ ΔACB nên

d) Xét tam giác vuông HNI và HFC ta có:

chung

Suy ra ΔHNI ᔕ ΔHFC (g.g)

Nên 

Xét tam giác HNF và HIC ta có:

 chung

⇒ ΔHNF ᔕ ΔHIC (c.g.c).