Bài 10 trang 85 Toán 8 Tập 2 Chân trời sáng tạo: Hình Thang & Tam Giác Đồng Dạng

Đề bài 10 trang 85 Toán 8

a) Cho hình thang ABCD (AB // CD), biết  (Hình 2a). Chứng minh rằng BD² = AB.CD.

b) Cho hình thang EFGH (EF // GH),  , EF = 9 m, GH = 16 m (Hình 2b). Tính độ dài x của HF.

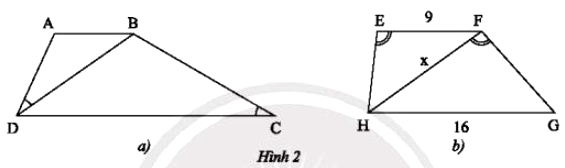
Phân tích đề bài và hướng giải quyết

Bài toán này yêu cầu chúng ta vận dụng kiến thức về tam giác đồng dạng để thiết lập các hệ thức giữa các cạnh, từ đó tìm ra kết quả cần chứng minh hoặc tính toán.

• Phần a: Dựa vào giả thiết về góc và tính chất song song của hình thang, chúng ta cần tìm ra hai tam giác đồng dạng chứa các cạnh BD, AB và CD. Từ đó, sử dụng tỉ số đồng dạng để suy ra đẳng thức cần chứng minh.

• Phần b: Tương tự, chúng ta sẽ áp dụng tính chất đồng dạng để tìm ra mối liên hệ giữa các cạnh đã cho (EF, GH) và cạnh cần tìm (HF).

Hướng dẫn giải bài 10 trang 85 Toán 8 - Lời giải chi tiết

a) Hướng dẫn chứng minh BD² = AB.CD

Xét ΔABD và ΔBDC có:

(gt)

(AB // CD, hai góc so le trong)

Vì vậy, ΔABD ᔕ ΔBDC (g.g)

Suy ra   (các cạnh tương ứng).

Vậy BD² = AB.CD (đpcm).

b) Hướng dẫn tính độ dài x của HF

 Tương tự câu a, ta có:

Xét ΔEFH và FHG ta có:

 (gt)

Nên ΔEFH ᔕ ΔFHG (g.g)

Suy ra  (các cạnh tương ứng).

Khi đó HF² = EF.GH = 9.16 = 144 

Vậy độ dài của HF = 12 cm.