Bài 11 trang 59 Toán 8 Tập 2 Chân trời sáng tạo: Bài Toán Thực Tế (Tam Giác Đồng Dạng)

Đề bài

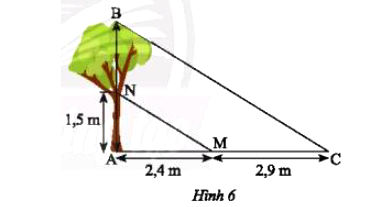
a) Độ cao AN và chiều dài bóng nắng của các đoạn thẳng AN, BN trên mặt đất được ghi lại như trong Hình 6. Tìm chiều cao AB của cái cây.

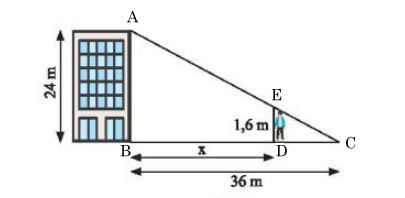
b) Một tòa nhà cao 24 m, đổ bóng nắng dài 36 m trên đường như Hình 7. Một người cao 1,6 m muốn đứng trong bóng râm của tòa nhà. Hỏi người đó có thể đứng cách tòa nhà xa nhất bao nhiêu mét?

Phân tích và hướng dẫn giải:

Để giải các bài toán này, chúng ta sử dụng kiến thức về tam giác đồng dạng.

• Tia nắng mặt trời là các đường thẳng song song.

• Chiều cao của vật thể và bóng của nó trên mặt đất tạo thành một tam giác vuông.

• Hai vật thể ở cùng một thời điểm sẽ tạo thành hai tam giác vuông đồng dạng.

Lời giải chi tiết:

a) Tìm chiều cao AB của cái cây

• Phân tích: Ta có hai tam giác vuông △A′B′C′ và $△ABC$ đồng dạng với nhau (với A′B′ là chiều cao người, B′C′ là bóng người, $AB$ là chiều cao cây, $BC$ là bóng cây).

• Lời giải: Theo hình vẽ, ta có: △ABC∼△A′B′C′

• 

  

  Vậy AB = 3,3125 m.

• Đáp số: Chiều cao của cái cây là khoảng 3,3125 m.

b) Tìm khoảng cách người đó có thể đứng cách tòa nhà xa nhất

• Phân tích: Ta có hai tam giác vuông $△ABC$ (tòa nhà) và △A′B′C′ (người) đồng dạng.

• Lời giải: Theo hình vẽ, ta có: △ABC∼△A′B′C′

•  

  

  Vậy, chiều dài bóng nắng của người đó là 2,4 m. Quãng đường người đó có thể đứng cách tòa nhà xa nhất là hiệu số giữa chiều dài bóng của tòa nhà và chiều dài bóng của người đó. Khoảng cách  (m).

• Đáp số: Người đó có thể đứng cách tòa nhà xa nhất 33,6 m.

Đáp số:

a) Chiều cao của cái cây là khoảng 3,3125 m

b) Người đó có thể đứng cách tòa nhà xa nhất 33,6 m.