Bài 10 trang 59 Toán 8 Tập 2 Chân trời sáng tạo

Đề bài:

Cho tam giác ABC và điểm D trên cạnh AB sao cho AD = 13,5 cm, DB = 4,5 cm. Tính tỉ số các khoảng cách từ các điểm D và B đến cạnh AC.

Phân tích và Hướng dẫn giải:

Đề bài cho tam giác $ABC$ với điểm $D$ nằm trên cạnh $AB$. Chúng ta biết độ dài hai đoạn $AD=13.5$ cm và $DB=4.5$ cm. Nhiệm vụ là tìm tỉ số khoảng cách từ điểm $D$ và điểm $B$ đến cạnh $AC$.

Để giải quyết bài toán này, chúng ta cần hình dung và vẽ các đường khoảng cách. Khoảng cách từ một điểm đến một đường thẳng chính là độ dài đoạn thẳng vuông góc kẻ từ điểm đó đến đường thẳng.

• Gọi $DH$ là khoảng cách từ điểm $D$ đến cạnh $AC$.

• Gọi $BK$ là khoảng cách từ điểm $B$ đến cạnh $AC$.

Vì cả $DH$ và $BK$ đều vuông góc với $AC$, nên chúng song song với nhau ($DH//BK$). Khi đó, ta có thể áp dụng hệ quả của định lý Thalès cho tam giác $ABK$ với đường thẳng $DH$ song song với cạnh $BK$.

Lời giải chi tiết:

Ta có hình minh hoạ như sau:

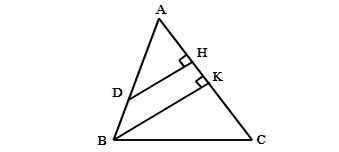
Gọi DH và BK lần lượt là khoảng cách từ D và B đến cạnh AC.

Ta có AB = AD + DB.

Khi đó AB = 13,5 + 4,5 = 18 (cm).

Vì DH // BK (cùng vuông góc với AC) nên áp dụng hệ quả định lí Thalès ta có:

Vậy tỉ số khoảng cách từ D và B đến cạnh AC là 3/4.