Hotline 0939 629 809

Bài 12 trang 59 Toán 8 Tập 2 Chân trời sáng tạo

09:42:3201/02/2024

Hướng dẫn giải bài 12 trang 59 Toán 8 tập 2 Chân trời sáng tạo nội dung SGK chi tiết dễ hiểu nhất giúp học sinh vận dụng giải Toán 8 Chân trời sáng tạo tập 2 tốt hơn, dễ dàng hơn.

Bài 12 trang 59 Toán 8 Tập 2 Chân trời sáng tạo:

Cho tam giác ABC có BC bằng 30 cm. Trên đường cao AH lấy các điểm K, I sao cho AK = KI = IH. Qua I và K vẽ các đường EF // BC, MN // BC (E, M ∈ AB; F, N ∈ AC).

a) Tính độ dài các đoạn thẳng MN và EF.

b) Tính diện tích tứ giác MNFE biết rằng diện tích tam giác ABC là 10,8 dm².

Giải bài 12 trang 59 Toán 8 Tập 2 Chân trời sáng tạo:

Ta có hình minh hoạ như sau:

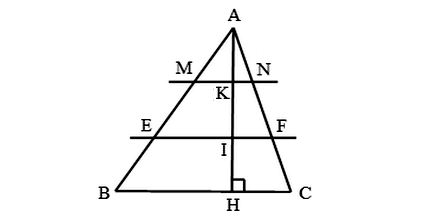
Giải bài 12 trang 59 Toán 8 Tập 2 Chân trời sáng tạo

a) Vì MN // BC, theo hệ quả định lí Thalès, ta có:

$\frac{MN}{BC}=\frac{AM}{AB}$ (1)

Trong tam giác ABH có MK // BH

$\Rightarrow \frac{AK}{AH}=\frac{AM}{AB}$ (2)

Từ (1) và (2) suy ra: $\frac{MN}{BC}=\frac{AK}{AH}$

Mà AK = KI = IH nên $\frac{AK}{AH}=\frac{1}{3}\Rightarrow \frac{MN}{BC}=\frac{1}{3}$

Suy ra: $MN=\frac{1}{3}BC=\frac{1}{3}.30=10\: (cm)$

Tam giác ABC có EF // BC nên: $\frac{EF}{BC}=\frac{AI}{AH}=\frac{2}{3}$ $\frac{E F}{B C} = \frac{A I}{A H} = \frac{2}{3}$

Suy ra: $EF=\frac{2}{3}BC=\frac{2}{3}.30=20\: (cm)$

Vậy MN = 10 cm và EF = 20 cm.

b) Đổi 10,8 dm²= 1080 cm².

MN // BC mà AH ⊥ BC nên AK ⊥ MN hay AK là đường cao của tam giác AMN.

Ta có: $AK=\frac{1}{3}AH$

$\frac{MN}{BC}=\frac{AK}{AH}=\frac{1}{3}\Rightarrow MN=\frac{1}{3}BC$

$S_{\Delta AMN}=\frac{1}{2}AK.MN=\frac{1}{2}.\frac{1}{3}AH.\frac{1}{3}BC$

$=\frac{1}{9}.\left ( \frac{1}{2}.AH.BC \right )=\frac{1}{9}.S_{\Delta ABC}$ $=\frac{1}{9}.1080=120\: (cm^2)$

Tương tự, có: $S_{\Delta AEF}=\frac{4}{9}S_{\Delta ABC}=\frac{4}{9}.1080=480\: (cm^2)$

Nên: S_MNEF = S_ΔAEF – S_ΔAMN = 480 – 120 = 360 (cm²)

Vậy diện tích tứ giác MNFE là 360 cm².

Với nội dung bài 12 trang 59 Toán 8 tập 2 Chân trời sáng tạo và cách giải chi tiết, dễ hiểu ở trên, Hay Học Hỏi hy vọng giúp các em nắm vững phương pháp giải Toán 8 Chân trời sáng tạo tập 2. Mọi góp ý và thắc mắc các em hãy để lại nhận xét dưới bài viết để được ghi nhận và hỗ trợ, chúc các em học tốt.

• Xem thêm giải Toán 8 Chân trời sáng tạo tập 2

> Bài 7 trang 59 Toán 8 Tập 2 Chân trời sáng tạo: Cho Hình 5, biết MN // DE, MN = 6 cm, MP = 3 cm, PE = 5 cm. Độ dài đoạn thẳng DE là...

> Bài 8 trang 59 Toán 8 Tập 2 Chân trời sáng tạo: Cho tam giác ABC, một đường thẳng song song với BC cắt AB và AC lần lượt tại D và E. Qua E kẻ...

> Bài 9 trang 59 Toán 8 Tập 2 Chân trời sáng tạo: Cho tam giác ABC biết AM là đường phân giác. Trong các khẳng định sau, khẳng định nào đúng?...

> Bài 10 trang 59 Toán 8 Tập 2 Chân trời sáng tạo: Cho tam giác ABC và điểm D trên cạnh AB sao cho AD = 13,5 cm, DB = 4,5 cm. Tính tỉ số các khoảng...

> Bài 11 trang 59 Toán 8 Tập 2 Chân trời sáng tạo: a) Độ cao AN và chiều dài bóng nắng của các đoạn thẳng AN, BN trên mặt đất được ghi lại như trong...

> Bài 12 trang 59 Toán 8 Tập 2 Chân trời sáng tạo: Cho tam giác ABC có BC bằng 30 cm. Trên đường cao AH lấy các điểm K, I sao cho AK = KI = IH. Qua I...