Bài 4 trang 91 Toán 8 Tập 2 Chân trời sáng tạo
Bài tập số 4, trang 91 SGK Toán 8 Tập 2 (Chân trời sáng tạo), là bài toán ứng dụng kiến thức Xác suất vào việc phân tích dữ liệu trên biểu đồ cột kép. Bài toán yêu cầu tính xác suất của các biến cố khác nhau khi chọn ngẫu nhiên một học sinh từ Câu lạc bộ Cờ vua của trường.
Bài 4 trang 91 Toán 8 Tập 2 Chân trời sáng tạo:
Số lượng học sinh tham gia Câu lạc bộ Cờ vua của một trường được biểu diễn ở biểu đồ sau:
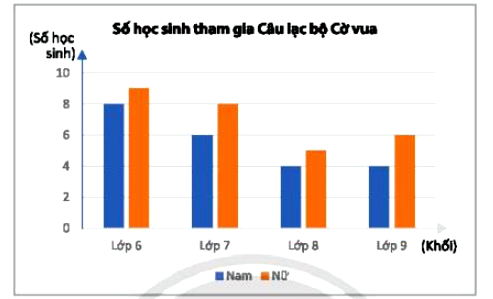
Chọn ngẫu nhiên 1 học sinh trong Câu lạc bộ Cờ vua của trường đó. Tính xác suất của các biến cố:
A: "Học sinh được chọn là nữ";
B: "Học sinh được chọn học lớp 8";
C: "Học sinh được chọn là nam và không học lớp 7".
Phân tích Dữ liệu và Không gian mẫu:
Dựa vào biểu đồ, ta tổng hợp số lượng học sinh Nam và Nữ theo từng khối lớp:
| Khối lớp | Số học sinh Nam | Số học sinh Nữ |
| Lớp 6 | 8 | 9 |
| Lớp 7 | 6 | 8 |
| Lớp 8 | 4 | 5 |
| Lớp 9 | 4 | 6 |
Tổng số học sinh (N):
Giải bài 4 trang 91 Toán 8 Tập 2 Chân trời sáng tạo:
Số học sinh tham gia Câu lạc bộ Cờ vua là 50 học sinh.
Số học sinh nữ tham gia Câu lạc bộ Cờ vua là:
9 + 8 + 5 + 6 = 28 (học sinh).
Khi đó, số kết quả thuận lợi của biến cố A là 28.
Xác suất biến cố A là: $P(A)=\frac{28}{50}=\frac{14}{25}$
Số học sinh lớp 8 tham gia Câu lạc bộ Cờ vua là:
4 + 5 = 9 (học sinh)
Khi đó, số kết quả thuận lợi của biến cố B là 9.
Xác suất biến cố B là:$P(B)=\frac{9}{50}$
Số học sinh nam không học lớp 7 tham gia Câu lạc bộ Cờ vua là:
8 + 4 + 4 = 16 (học sinh)
Khi đó, số kết quả thuận lợi của biến cố C là 16.
Xác suất biến cố C là: $P(C)=\frac{16}{50}=\frac{8}{25}$
Bài toán tính xác suất dựa trên biểu đồ cột kép đã được giải quyết bằng việc xác định số kết quả thuận lợi cho từng biến cố trên tổng số 50 học sinh. Xác suất để chọn được học sinh nữ là $14/25$, đây là xác suất cao nhất trong các biến cố.
Xác suất để học sinh được chọn thuộc lớp 8 là $9/50$, và xác suất để chọn được học sinh nam nhưng không phải lớp 7 là $8/25$. Việc phân tích dữ liệu từ biểu đồ thành số lượng cụ thể cho từng nhóm là bước then chốt để áp dụng chính xác công thức xác suất.
• Xem thêm:
Đánh giá & nhận xét
-
 Bài 11 trang 96 Toán 8 Tập 2 Chân trời sáng tạo
Bài 11 trang 96 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 10 trang 96 Toán 8 Tập 2 Chân trời sáng tạo
Bài 10 trang 96 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 9 trang 96 Toán 8 Tập 2 Chân trời sáng tạo
Bài 9 trang 96 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 7 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
Bài 7 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 6 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
Bài 6 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 5 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
Bài 5 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 4 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
Bài 4 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 3 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
Bài 3 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 2 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
Bài 2 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 1 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
Bài 1 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 7 trang 28 Toán 8 Tập 2 Chân trời sáng tạo
Bài 7 trang 28 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 6 trang 28 Toán 8 Tập 2 Chân trời sáng tạo
Bài 6 trang 28 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 5 trang 28 Toán 8 Tập 2 Chân trời sáng tạo
Bài 5 trang 28 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 4 trang 28 Toán 8 Tập 2 Chân trời sáng tạo
Bài 4 trang 28 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 3 trang 28 Toán 8 Tập 2 Chân trời sáng tạo
Bài 3 trang 28 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 2 trang 28 Toán 8 Tập 2 Chân trời sáng tạo: Độ dài đoạn thẳng
Bài 2 trang 28 Toán 8 Tập 2 Chân trời sáng tạo: Độ dài đoạn thẳng
-
 Bài 1 trang 28 Toán 8 Tập 2 Chân trời sáng tạo
Bài 1 trang 28 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 6 trang 66 Toán 8 Tập 2 Chân trời sáng tạo
Bài 6 trang 66 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 5 trang 66 Toán 8 Tập 2 Chân trời sáng tạo
Bài 5 trang 66 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 4 trang 66 Toán 8 Tập 2 Chân trời sáng tạo
Bài 4 trang 66 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 3 trang 65 Toán 8 Tập 2 Chân trời sáng tạo
Bài 3 trang 65 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 2 trang 65 Toán 8 Tập 2 Chân trời sáng tạo
Bài 2 trang 65 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 1 trang 65 Toán 8 Tập 2 Chân trời sáng tạo
Bài 1 trang 65 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 4 trang 94 Toán 8 Tập 2 Chân trời sáng tạo
Bài 4 trang 94 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 3 trang 94 Toán 8 Tập 2 Chân trời sáng tạo
Bài 3 trang 94 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 2 trang 94 Toán 8 Tập 2 Chân trời sáng tạo
Bài 2 trang 94 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 1 trang 94 Toán 8 Tập 2 Chân trời sáng tạo
Bài 1 trang 94 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 8 trang 40 Toán 8 Tập 2 Chân trời sáng tạo
Bài 8 trang 40 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 7 trang 40 Toán 8 Tập 2 Chân trời sáng tạo
Bài 7 trang 40 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 6 trang 40 Toán 8 Tập 2 Chân trời sáng tạo
Bài 6 trang 40 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 5 trang 40 Toán 8 Tập 2 Chân trời sáng tạo
Bài 5 trang 40 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 4 trang 40 Toán 8 Tập 2 Chân trời sáng tạo
Bài 4 trang 40 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 3 trang 40 Toán 8 Tập 2 Chân trời sáng tạo
Bài 3 trang 40 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 2 trang 39 Toán 8 Tập 2 Chân trời sáng tạo: Bài Toán Lập Phương Trình
Bài 2 trang 39 Toán 8 Tập 2 Chân trời sáng tạo: Bài Toán Lập Phương Trình
-
 Bài 1 trang 39 Toán 8 Tập 2 Chân trời sáng tạo
Bài 1 trang 39 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 8 trang 84 Toán 8 Tập 2 Chân trời sáng tạo
Bài 8 trang 84 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 7 trang 84 Toán 8 Tập 2 Chân trời sáng tạo
Bài 7 trang 84 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 6 trang 84 Toán 8 Tập 2 Chân trời sáng tạo
Bài 6 trang 84 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 5 trang 84 Toán 8 Tập 2 Chân trời sáng tạo
Bài 5 trang 84 Toán 8 Tập 2 Chân trời sáng tạo

















































