Bài 3 trang 76 Toán 8 Tập 2 Chân trời sáng tạo

Bài 3 trang 76 Toán 8 Tập 2 Chân trời sáng tạo: 

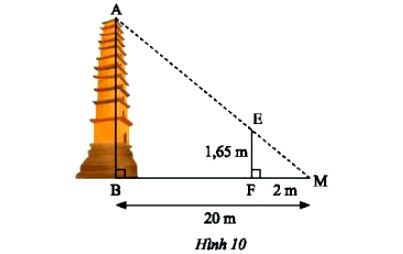
Trong Hình 10, biết MB = 20m, MF = 2m, EF = 1,65 m. Tính chiều cao AB của ngọn tháp.

Phân Tích và Hướng Dẫn Giải:

1. Mô hình Tam giác vuông: Ta có $\triangle MEF$ và $\triangle MAB$ đều là tam giác vuông (giả sử tháp $AB$ và cọc $EF$ đều vuông góc với mặt đất $MB$).

   $\Rightarrow \widehat{MAB} = \widehat{MEF} = 90^\circ$

2. Chứng minh Đồng dạng: Hai tam giác $\triangle MEF$ và $\triangle MAB$ đồng dạng theo trường hợp g.g (do có một cặp góc vuông và một góc chung $\widehat{M}$).

3. Thiết lập Tỉ lệ thức: Sử dụng tỉ số đồng dạng để tính cạnh $AB$:

   $\frac{EF}{AB} = \frac{MF}{MB}$

4. Tính $AB$: Thay số và giải phương trình.

Giải bài 3 trang 76 Toán 8 Tập 2 Chân trời sáng tạo: 

Xét ta giác vuông MEF và MAB ta có:

$\widehat{M}$ chung

Suy ra ΔMEF ᔕ ΔMAB (g.g)

nên $\frac{EF}{AB}=\frac{MF}{MB}$ (các cạnh tương ứng).

Khi đó $\frac{1,65}{AB}=\frac{2}{20}$ $\Rightarrow AB=\frac{1,65.20}{2}=16,5\: (cm)$

Vậy AB = 16,5 (cm).