Bài 8 trang 72 Toán 8 Tập 2 Chân trời sáng tạo

Bài 8 trang 72 Toán 8 Tập 2 Chân trời sáng tạo: 

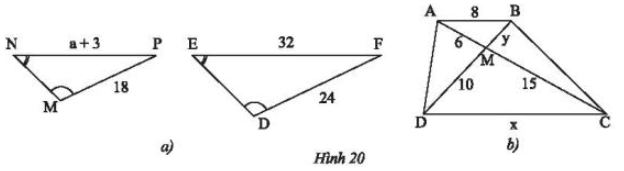
a) Trong Hình 20a, cho biết $\widehat{N}=\widehat{E}$, $\widehat{M}=\widehat{D}$ , MP = 18 m, DF = 24 m, EF = 32 m, NP = a + 3 (m). Tìm a.

b) Cho ABCD là hình thang (AB // CD) (Hình 20b).

Chứng minh rằng ΔAMB ᔕ ΔCMD. Tìm x, y.

Phân Tích Hướng Dẫn Giải:

1. Phần (a):

   • Chứng minh $\triangle MNP \sim \triangle DEF$ theo trường hợp g.g.

   • Sử dụng tỉ số đồng dạng để lập phương trình theo $a$: $\frac{NP}{EF} = \frac{MP}{DF}$.

2. Phần (b):

   • Chứng minh $\triangle AMB \sim \triangle CMD$ (g.g) bằng cách sử dụng các cặp góc so le trong tạo bởi $AB // CD$.

   • Sử dụng tỉ số đồng dạng để lập hệ phương trình tìm $x$ và $y$: $\frac{AM}{CM} = \frac{MB}{MD} = \frac{AB}{CD}$.

Giải bài 8 trang 72 Toán 8 Tập 2 Chân trời sáng tạo: 

a) Xét ΔMNP và ΔDEF có:

$\widehat{N}=\widehat{E}$, $\widehat{M}=\widehat{D}$ 

Vì vậy: ΔMNP ᔕ ΔDEF (g.g)

Suy ra $\frac{NP}{EF}=\frac{MP}{DF}$ (các cạnh tương ứng).

Khi đó $\frac{a+3}{32}=\frac{18}{24}=\frac{3}{4}$  nên $a+3=\frac{32.3}{4}=24\: (cm)$

Vậy a = 24 – 3 = 21.

b) Xét hình thang ABCD (AB // CD):

Vì AB // CD nên:

$\widehat{MAB}=\widehat{MCD}$, $\widehat{MBA}=\widehat{MDC}$ (cặp góc so le trong).

Xét ΔAMB và ΔCMD có:

$\widehat{MAB}=\widehat{MCD}$ (chứng minh trên)

$\widehat{MBA}=\widehat{MDC}$ (chứng minh trên)

Do đó ΔAMB ᔕ ΔCMD (g.g)

Suy ra  $\frac{AM}{CM}=\frac{MB}{MD}=\frac{AB}{CD}$ (các cặp cạnh tương ứng).

Khi đó $\frac{6}{15}=\frac{y}{10}=\frac{8}{x}$

Suy ra: $x=\frac{15.8}{6}=20$; $y=\frac{6.10}{15}=4$

Vậy x = 20; y = 4.