Bài 10 trang 72 Toán 8 Tập 2 Chân trời sáng tạo

Bài 10 trang 72 Toán 8 Tập 2 Chân trời sáng tạo: 

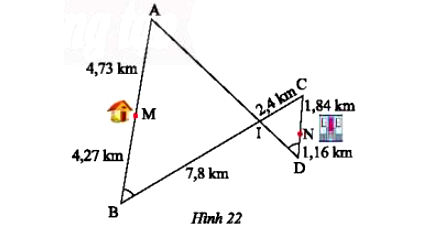
Đường đi và khoảng cách từ nhà anh Thanh (điểm M) đến công ty (điểm N) được thể hiện trong Hình 22. Hãy tìm con đường ngắn nhất để đi từ nhà của anh Thanh đến công ty.

Phân tích và Hướng dẫn Giải:

1. Dữ liệu đã biết (giả sử từ hình vẽ):

   • $MA = 4,73$

   • $MB = 4,27$

   • $NC = 1,84$

   • $ND = 1,16$

   • $AB = 9 \text{ km}$

   • $IB=7,8$

   • $CD = 3$

   • Góc $\widehat{B} = \widehat{D}$ và $\widehat{AIB} = \widehat{CID}$.

2. Mục tiêu: Tính độ dài các đoạn thẳng $IA, IB, IC, ID$ và so sánh các lộ trình qua $I$.

3. Lộ trình khả thi: Mọi lộ trình đều phải đi qua điểm giao cắt $I$. Tổng lộ trình = $(\text{Đường từ } M \text{ đến } I) + (\text{Đường từ } I \text{ đến } N)$.

Giải bài 10 trang 72 Toán 8 Tập 2 Chân trời sáng tạo: 

Xét ΔIAB và ΔICD ta có:

$\widehat{B}=\widehat{D}$ (gt)

$\widehat{AIB}=\widehat{CID}$ (đối đỉnh)

Suy ra ΔIAB ᔕ ΔICD (g.g) nên

$\frac{IA}{TC}=\frac{IB}{ID}=\frac{AB}{CD}$

⇒ IA = 7,2; ID = 2,6

Quãng đường đi từ M → A → I là:

4,73 + 7,2 = 11,93 (km)

Quãng đường đi từ M → B → I là:

4,27 + 7,8 = 12,07 (km)

Quãng đường đi từ I → C → N là:

2,4 + 1,84 = 4,24 (km)

Quãng đường đi từ I → D → N là:

2,6 + 1,16 = 3,76 (km)

Vậy quãng đường ngắn nhất để đi từ nhà của anh Thanh đến công ty là M → A → I → D → N với độ dài 15,69 km.